Уравнения КТ 1
Решение уравнения $$x^2 + 2x - x(x + 2) = 0$$ имеет вид:
$$x^2 + 2x - x^2 - 2x = 0$$,
$$0 = 0$$,
$$x \in R$$.
Количество различных корней уравнения $$\left(2,5^{6|x|}\right)^{-1} = \left(0,4^x\right)^{2x}$$ равно:
$$\left(\frac{5}{2}\right)^{-6|x|} = \left(\frac{2}{5}\right)^{2x^2}$$, $$\left(\frac{2}{5}\right)^{6|x|} = \left(\frac{2}{5}\right)^{2x^2}$$,
$$6|x| = 2|x|^2$$, $$|x|^2 - 3|x| = 0$$, $$|x|(|x| - 3) = 0$$,
откуда $$|x| = 0$$ или $$|x| = 3$$.
Тогда, $$x = 0$$ или $$x = \pm3$$.
Произведение всех целых значений $$a$$, при которых уравнение $$|x^2 - 6x + 8| = \frac{a}{6}$$ имеет четыре решения, равно:
-
Построим параболу $$y = x^2 - 6x + 8$$ (1) (рис. 1).
Координаты вершины:
$$x_0 = \frac{-b}{2a} = 3$$, $$y_0 = 9 - 18 + 8 = -1$$.
Нули функции: $$x_1 = 2$$, $$x_2 = 4$$.
-
Построим график функции $$y = |x^2 - 5x + 6|$$ (2): часть графика (1), расположенного над ось Ох, оставляем, а ту, что под осью, отражаем симметрично этой оси (рис. 2).
-
Построим прямую $$y = \frac{a}{b}$$ (3) так, чтобы она пересекала график (2) в четырех точках (рис. 2).
Очевидно, что $$0 < \frac{a}{b} < 1$$, откуда $$0 < a < 6$$.
Тогда, $$1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 = 120$$.
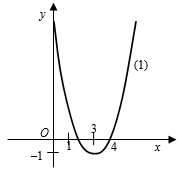
Рис. 1
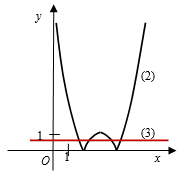
Рис. 2
Число, обратное корню уравнения $$log_5x + log_{25}x + log_{125}x = -\frac{11}{3}$$, равно:
ОДЗ: $$x > 0$$.
$$log_5x + \frac{1}{2}log_5x + \frac{1}{3}log_5x = -\frac{11}{3}$$,
$$\frac{11}{6}log_5x = -\frac{11}{3}$$, $$log_5x = -2$$, $$x = \frac{1}{25}$$.
Тогда, $$\left(\frac{1}{25}\right)^{-1} = 25$$.
Сумма корней (или корень, если он единственный) уравнения $$|x^2 + 2x + 1| - |x^2 + 2x| - 3x = 0$$ равна:
$$|(x + 1)^2| - |x^2 + 2x| - 3x = 0$$,
$$(x + 1)^2 - |x^2 + 2x| - 3x = 0$$,
$$|x^2 + 2x| = x^2 - x + 1$$, где $$x^2 - x + 1 \ge 0$$,
$$(x^2 + 2x)^2 - (x^2 - x + 1)^2 = 0$$,
$$(3x - 1)(2x^2 + x + 1) = 0$$,
откуда $$3x - 1 = 0$$ или $$2x^2 + x + 1 = 0$$, где $$D < 0$$.
Получим: $$x = \frac{1}{3}$$.
Если $$(x_0;y_0)$$ – решение системы уравнений $$\left\{\begin{array}{l} x - 4y = 11, \\ \sqrt{x} + 2\sqrt{y} = 11, \end{array}\right.$$ то значение выражения $$(x_0y_0)^{0,5}$$ равно:
$$\left\{\begin{array}{l} (\sqrt{x} - 2\sqrt{y})(\sqrt{x} + 2\sqrt{y} = 11, \\ \sqrt{x} + 2\sqrt{y} = 11; \end{array}\right.$$ $$\left\{\begin{array}{l} \sqrt{x} - 2\sqrt{y} = 1, \\ \sqrt{x} + 2\sqrt{y} = 11; \end{array}\right.$$
$$\left\{\begin{array}{l} \sqrt{x} - 2\sqrt{y} = 1, \\ 2\sqrt{x} = 12; \end{array}\right.$$ $$\left\{\begin{array}{l} \sqrt{y} = 2,5, \\ \sqrt{x} = 6; \end{array}\right.$$ $$\left\{\begin{array}{l} y = 6,25, \\ x = 36. \end{array}\right.$$
Тогда, $$\sqrt{6,25 \cdot 36} = 2,5 \cdot 6 = 15$$.
Количество всех корней уравнения $$\frac{x + 2}{x^2 + 1} = \frac{x + 2}{x^2 - 1}$$ равно:
$$\frac{x + 2}{x^2 + 1} - \frac{x + 2}{x^2 - 1} = 0$$,
$$(x + 2) \cdot \left(\frac{1}{x^2 + 1} - \frac{1}{x^2 - 1}\right) = 0$$,
$$(x + 2) \cdot \frac{-2}{(x^2 + 1)(x^2 - 1)} = 0$$,
откуда $$x = -2$$.
Частное от деления наибольшего и наименьшего корней уравнения $$sin(5x - 2,5\pi) - cos(15x - 9\pi) = sin5x - sin15x$$, принадлежащих интервалу $$(-0,2\pi; 0,4\pi)$$, равно:
-
$$-sin(0,5\pi - 5x) - cos(\pi + 15x) = sin5x - sin15x$$,
$$cos15x - cos5x = sin5x - sin15x$$,
$$-2sin10x \cdot sin5x = -2sin5x \cdot cos10x$$,
$$sin5x(sin10x - cos10x) = 0$$, откуда:
- $$sin5x = 0$$, $$x = \frac{\pi n}{5}$$, где $$n \in Z$$;
- $$tg10x = 1$$, $$x = \frac{\pi}{40} + \frac{\pi m}{10}$$, где $$m \in Z$$.
-
Отбор корней:
если $$m = -2$$, то $$x = -\frac{7\pi}{40}$$;
если $$m = -1$$, то $$x = \frac{13\pi}{40}$$.
- $$\frac{13\pi}{40} : \left(-\frac{7\pi}{40}\right) = -\frac{13}{7}$$.
Если $$x_1$$ и $$x_2$$ – корни уравнения $$x^{2log_3x} = 10^{lg9}$$, то значение выражения $$10(x_1 + x_2)^{-1}$$ равно:
Пусть $$log_3x = a$$, откуда $$x = 3^a$$.
Получим:
$$(3^a)^{2a} = 9$$, $$3^{2a^2} = 3^2$$, $$2a^2 = 2$$, $$a = \pm1$$.
Тогда: $$x_1 = 3$$, $$x_2 = \frac{1}{3}$$; $$10 \cdot \left(3 + \frac{1}{3}\right)^{-1} = 3$$.
Корень уравнения $$\sqrt{27^{1 + 2x}} = \sqrt[3]{81^{x - 3}}$$ не превосходит число:
$$3^{3(1 + 2x)\frac{1}{2}} = 3^{4(x - 3)\frac{1}{3}}$$, $$\frac{3 + 6x}{2} = \frac{4x - 12}{3}$$,
$$9 + 18x = 8x - 24$$, $$x = -3,3$$.

