Текстовые задачи КТ 1
Два насоса, работая одновременно, наполняют бассейн за $$3$$ ч $$44$$ мин. Работая раздельно, первый насос наполнит бассейн на $$60$$ мин быстрее, чем второй. Второй насос наполнит бассейн за:
Пусть $$a$$ – объем бассейна.
Раздельная работа:

Совместная работа:
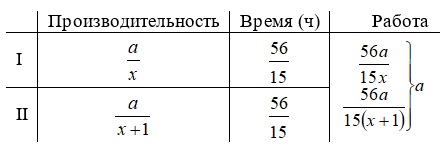
Решим уравнение:
$$\frac{56a}{15x}+\frac{56a}{15\left ( x+1 \right )}=a$$;
$$\frac{1}{x}+\frac{1}{\left ( x+1 \right )}=\frac{15}{56}$$;
$$\frac{2x+1}{x\left ( x+1 \right )}=\frac{15}{56}$$;
$$15x^{2}-97x-56=0$$,
откуда $$D=113^{2}$$, $$x_{1}=-\frac{8}{15}$$ (посторонний корень), $$x_{2}=7$$.
Тогда, $$t_{2}=7+1=8$$ (ч).
Два мальчика одновременно на велосипедах направляются к речке соответственно со скоростями движения $$16$$ км/ч и $$15$$ км/ч. Через $$10$$ минут первый мальчик делает остановку на $$5$$ минут, а затем продолжает путь с первоначальной скоростью и догоняет второго мальчика после остановки через:
Пусть первый мальчик догонит второго через $$x$$ часов.
Первый мальчик:
$$v_{1}=16$$ (км/ч); $$t_{1}=\left ( \frac{1}{6}+x \right )$$ (ч);
$$S_{1}=16\cdot \left ( \frac{1}{6}+x \right )$$ (км).
Второй мальчик:
$$v_{2}=15$$ (км/ч); $$t_{2}=\left ( \frac{10}{60}+\frac{5}{60}+x \right )=\left ( \frac{1}{4}+x \right )$$ (ч);
$$S_{2}=15\cdot \left ( \frac{1}{4}+x \right )$$ (км).
Так как $$S_{1}=S_{2}$$, то
$$16\cdot \left ( \frac{1}{6}+x \right )=15\cdot \left ( \frac{1}{4}+x \right )$$,
$$\frac{8}{3}+16x=\frac{15}{4}+15x$$,
$$x=\frac{15}{4}-\frac{8}{3}=\frac{45-32}{12}=\frac{13}{12}=1\frac{5}{60}$$ (ч).
Если свежескошенная трава содержит по массе $$80$$ % воды, а сено – $$20$$ %, то чтобы получить $$1$$ т $$200$$ кг сена, масса скошенной травы должна составить:
Масса воды в сене:
$$1200:100\cdot 20=240$$ (кг).
Масса травяного вещества в сене и в траве:
$$1200-240=960$$ (кг).
Масса травы:
$$960:\left ( 100-80 \right )\cdot 100=4800$$ (кг).
Если на экзамене по математике за курс средней школы ученик получил оценку $$8$$,
а на ЦТ – на $$15$$ % ниже, то его оценка на ЦТ составила:
$$8:100\cdot \left ( 100-15 \right )=0,08\cdot 85=6,8$$.
Если от числа, сумма цифр которого равна $$14$$, отнять число $$36$$ и получить число, записанное теми же цифрами, но в обратном порядке, то искомое число будет равно:
Пусть $$\overline{ab}$$ – искомое число.
Получим:
$$\begin{cases} a+b=14,\\ \overline{ab}-36=\overline{ba}; \end{cases} \begin{cases} a+b=14,\\ 10a+b-36=10b+a;\end{cases} \begin{cases} a+b=14,\\ 9a-9b=36; \end{cases}$$
$$\begin{cases} a+b=14,\\ a-b=4; \end{cases} \begin{cases} a+b=14,\\ 2a=18;\end{cases} \begin{cases} b=5,\\ a=9.\end{cases}$$.
Тогда, $$\overline{ab}=95$$.
Первая и третья бригады прокладывают за $$10$$ дней $$10$$ км газопровода. Работая одновременно, три бригады проложат за этот срок в $$1\frac{4}{11}$$ раза больше газопровода, чем при совместной работе проложат первые две. Так как вторая бригада совместно с третьей прокладывает газопровод в $$1,8$$ раза быстрее, чем самостоятельно, то за $$20$$ дней она может уложить газопровод длиной (в км):
- $$\left ( v_{1}+v_{3} \right )\cdot 10=10$$, откуда $$v_{1}+v_{3}=1$$.
-
$$v_{1}+v_{2}+v_{3}=\frac{15}{11}\left ( v_{1}+v_{2} \right )$$,
$$1+v_{2}=\frac{15}{11}\left ( v_{1}+v_{2} \right )$$,
$$15v_{1}+4v_{2}=11$$. - $$v_{2}+v_{3}=1,8v_{2}$$, откуда $$v_{3}=0,8v_{2}$$.
Запишем систему уравнений:
$$v_{1}+v_{3}=1$$; $$15v_{1}+4v_{2}=11$$; $$v_{3}=0,8v_{2}$$.
Тогда: $$v_{1}+0,8v_{2}=1
$$, откуда $$15v_{1}+12v_{2}=15$$.
Вычтем из уравнения $$15v_{1}+12v_{2}=15$$ уравнение $$15v_{1}+4v_{2}=11$$.
Получим: $$8v_{2}=4$$, откуда $$v_{2}=0,5$$.
Следовательно, $$0,5\cdot 20=10$$ (км).
Чтобы при смешивании $$30$$ %-го раствора соли в воде с $$10$$ %-ным раствором получить $$800$$ г
$$12$$ %–го раствора, первого раствора необходимо взять (в граммах):
Пусть первого раствора взяли $$x$$ г, тогда второго взяли $$\left ( 800-x \right )$$ г.
Решим уравнение:
$$0,3x+0,1\left ( 800-x \right )=0,12\cdot 800$$,
$$0,3x+80-0,1x=96$$,
$$0,2x=16$$, откуда $$x=80$$ (г).
Числитель правильной несократимой дроби увеличили на $$2$$, а ее знаменатель – в $$2$$ раза. Так как разность этой дроби и полученной равна $$\frac{1}{6}$$, а их сумма равна $$\frac{17}{18}$$, то знаменатель этой дроби больше ее числителя на:
Искомая дробь: $$\frac{a}{b}$$, где $$a< b$$.
Новая дробь: $$\frac{a+2}{2b}$$.
Составим уравнения:
- $$\frac{a}{b}-\frac{a+2}{2b}=\frac{1}{6}$$; $$\frac{2a-a-2}{2b}=\frac{1}{6}$$; $$\frac{a-2}{b}=\frac{1}{3}$$; $$b=3a-6$$;
- $$\frac{a}{b}+\frac{a+2}{2b}=\frac{17}{18}$$; $$\frac{2a+a+2}{2b}=\frac{17}{18}$$; $$\frac{3a+2}{b}=\frac{17}{9}$$; $$17b=27a-18$$.
$$ 15a-102=27a+18$$,
$$24a=120$$,
$$a=5$$, $$b=9$$.
Откуда $$9-5=4$$.
Из пунктов $$A$$ и $$B$$ одновременно навстречу друг другу отправились пешеход и велосипедист и встретились через $$50$$ мин. Продолжая движение в том же направлении, велосипедист прибыл в пункт $$A$$ на $$4$$ ч раньше, чем пешеход прибыл в пункт $$B$$. Пешеход находился в пути (в часах):
Пусть $$v_{п}=x$$ (км/ч), а $$v_{в}=у$$ (км/ч).
Тогда: $$S=\frac{5\left ( x+y \right )}{6}$$ (км);
$$t_{п}=\frac{5\left (x+y \right )}{6x}=\frac{5}{6}\left ( 1+\frac{y}{x} \right )$$,
$$t_{в}=\frac{5\left (x+y \right )}{6y}=\frac{5}{6}\left ( \frac{x}{y}+1 \right )$$.
Решим уравнение:
$$\frac{5}{6}\left (1+ \frac{y}{x} \right )=\frac{5}{6}\left ( 1+\frac{x}{y} \right )+4$$.
Полагая $$\frac{y}{x}=a$$, получим:
$$5\left ( 1+a \right )=5\left ( 1+\frac{1}{a} \right )+24$$,
$$5+5a=5+\frac{5}{a}+24$$,
$$5a^{2}-24a-5=0$$,
откуда $$D=26^{2}$$,
$$a_{1}=-0,2$$ (посторонний корень), $$a_{2}=5$$.
Тогда, $$t_{п}=\frac{5}{6}\left ( 1+5 \right )=5$$ (ч).
Если цифра десятков двузначного числа на $$2$$ меньше цифры единиц, а произведение этого числа и суммы его цифр равно $$460$$, то это число равно:
Пусть $$\overline{ab}$$ – искомое число.
Получим: $$
\begin{cases} a+b=2,\\ \overline{ab} \cdot\left ( a+b \right )=640. \end{cases} $$
Решим уравнение:
$$\left ( 10a+b \right )\left ( a+b \right )=640$$;
$$\left (11b+20 \right )\left ( 2b+2 \right )=640$$;
$$\left (11b+20 \right )\left ( b+1 \right )=320$$;
$$11^{2}+31b-300=0$$,
откуда $$D=119^{2}$$, $$b_{1}=-\frac{75}{11}$$ (посторонний корень), $$b_{2}=4$$.
Тогда, $$a=6$$. Искомое число: $$64$$.

