Текстовые задачи КТ 2
По окружности длиной $$10$$ м одновременно в одном направлении из одного и того же пункта начали движение две точки. Так как первая точка движется со скоростью $$2$$ м/мин и скорость ее движения составляет $$44\frac{4}{9}$$ % от скорости движения второй точки, то время (в минутах), через которое точки встречаются, равно:
Пусть $$x$$ мин – время, через которое точки встретятся.
Найдем скорость движения второй точки:
$$2=\frac{400v_{2}}{9\cdot 100}$$, $$1=\frac{2v_{2}}{9}$$, $$v_{2}=4,5$$ (км/ч).
Заполним таблицу:

Так как скорость второй точки больше скорости первой, то до встречи она проходит расстояние на $$10$$ м (длину окружности) большее, чем первая точка.
Получим уравнение:
$$2x+10=4,5x$$, откуда $$x=4$$ (мин).
Катер, собственная скорость движения которого равна $$24,5$$ км/ч, спустился вниз по течению реки от пристани $$A$$ к пристани $$B$$ и вернулся в пристань $$A$$ за $$6$$ ч $$25$$ мин, пройдя при этом путь длиной в $$154$$ км. Скорость течения реки была равна:
Пусть скорость течения реки равна $$x$$ км/ч.
Заполним таблицу:
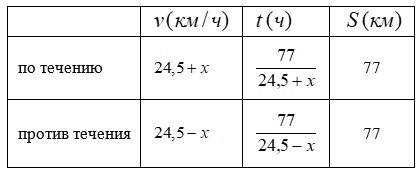
$$\frac{77}{24,5+x}+\frac{77}{24,5-x}=\frac{77}{12}$$,
$$\frac{1}{24,5+x}+\frac{1}{24,5-x}=\frac{1}{12}$$,
$$\frac{2,5-x+24,5+x}{\left ( 24,5+x \right )\left ( 24,5-x \right )}=\frac{1}{12}$$,
$$\frac{49}{\left ( 24,5 \right )^{2}-x^{2}}=\frac{1}{12}$$,
$$\frac{49^{2}}{4}-x^{2}=49\cdot 12$$,
$$x^{2}=\frac{49^{2}-49\cdot 48}{4}=\frac{49}{4}$$,
откуда $$x=3,5$$.
Из города $$A$$ в город $$B$$ выехал мотоциклист. Через полчаса из города $$B$$ со скоростью, превышающей скорость мотоциклиста в полтора раза, в город $$A$$ выехал автомобиль и встретил мотоциклиста в $$48$$ км от города $$B$$. Если бы они выехали одновременно, то встретились бы в $$40$$ км от города $$A$$. Скорость (в км/ч) мотоциклиста была равна:
Пусть $$v_{м}=x$$ (км/ч), $$v_{a}=1,5x$$ (км/ч), $$S$$ км – расстояние между городами.
Решим систему уравнений:
$$\begin{cases} \frac{S-48}{x}=\frac{48}{1,5x}+\frac{1}{2},\\ \frac{40}{x}=\frac{S-40}{1,5x}; \end{cases}
\begin{cases} \frac{S-48}{x}-\frac{32}{x}=\frac{1}{2},\\ \frac{20}{x}=\frac{S-40}{3x}; \end{cases}
\begin{cases} \frac{S-80}{x}=\frac{1}{2},\\ S=100; \end{cases}
\begin{cases} x=40,\\ S=100. \end{cases}
$$
Два пешехода одновременно выходят навстречу друг другу и встречаются через $$2$$ ч, пройдя $$18$$ км. Так как скорость первого пешехода больше скорости второго на $$2$$ км/ч, то среднее арифметическое их скоростей равно:
Пусть $$v_{2}=x$$ км/ч, тогда $$v_{1}=\left ( x+1 \right )$$ км/ч.
Тогда: $$\left ( x+x+1 \right )\cdot 2=18$$, откуда $$x=4$$.
Следовательно, $$\frac{v_{1}+v_{2}}{2}=\frac{5+4}{2}=4,5$$ (км/ч).
Если число студентов факультета, увеличиваясь ежегодно на один и тот же процент, возросло за два года с $$5 000$$ до $$6 050$$ человек, то ежегодно количество студентов (в процентах) увеличивалось на:
Пусть число студентов ежегодно увеличивалось на $$x$$ %.
Число студентов за первый год составило:
$$\left ( 100+x \right )$$% от $$5000$$ или $$\frac{5000\cdot \left ( 100+x \right )}{100}$$.
Число студентов за второй год составило:
$$\left ( 100+x \right )$$% от $$\frac{5000\cdot \left ( 100+x \right )}{100}$$ или
$$6050=\frac{5000\cdot \left ( 100+x \right )\cdot \left ( 100+x \right )}{100\cdot 100}$$,
$$121=\frac{\left ( 100+x \right )^{2}}{100}$$,
$$\left ( 100+x \right )^{2}=121\cdot 100$$,
откуда $$100+x=110$$, $$x=10$$ (%).
Каждый из двух токарей вытачивает по $$180$$ деталей. Первый токарь вытачивает $$5$$ деталей за то же время, за которое второй вытачивает $$4$$ детали. Так как первый токарь закончил работу на $$3$$ часа быстрее второго, то количество деталей, выточенных им за час, равно:
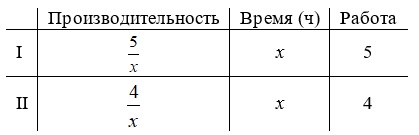
Решим уравнение:
$$180:\frac{5}{x}+3=180:\frac{4}{x}$$,
$$\frac{180x}{5}+3=\frac{180x}{4}$$,
$$36x+3=45x$$, откуда $$x=\frac{1}{3}$$.
Тогда, $$\frac{5}{x}=5\cdot 3=15$$ (дет.).
При подготовке к экзамену ученик запланировал учить в день определенное количество экзаменационных вопросов. Но так как он начал подготовку к экзамену на $$2$$ дня позже намеченного срока, то чтобы успеть подготовить все $$40$$ вопросов, вынужден был учить в день на один вопрос больше, чем запланировал. Число вопросов, которые запланировал учить в один день ученик, равно:

Решим уравнение:
$$\frac{40}{x}-\frac{40}{x+1}=2$$; $$\frac{1}{x}-\frac{1}{x+1}=\frac{1}{20}$$; $$\frac{1}{x\left ( x+1 \right )}=\frac{1}{20}$$, $$x^{2}+x-20=0$$,
откуда $$x_{1}=-5$$ (посторонний корень), $$x_{2}=4$$ – запланированное число вопросов.

