Планиметрия КТ 2
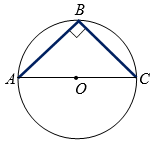
Если вписанный в окружность угол $$ABC$$ – прямой, а каждая из хорд $$AB$$ и $$BC$$ равна $$2\sqrt{2}$$, то площадь кругового сектора, ограниченного радиусами $$OA$$ и $$OC$$ и дугой окружности $$AC$$, равна:
По теореме Пифагора (рис. 2): $$AC=\sqrt{8+8}=4$$.
Тогда, $$OA=AC:2=2=R$$.
Площадь круга: $$S=\pi R^2 = 4\pi$$.
Площадь сектора: $$S=4\pi : 2 = 2\pi$$.
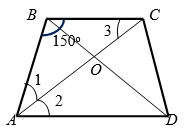
Если один из углов равнобедренной трапеции равен $$150^{\circ}$$, а ее диагональ является биссектрисой острого угла, то диагонали трапеции пересекаются под углом, градусная мера которого равна:
- На рисунке 5:
$$\angle 1 = \angle 2 = \angle 3$$, следовательно, $$\angle 3 = (180^{\circ} - 150^{\circ}):2=15^{\circ}$$.
- Так как $$OC=OB$$, то $$\angle CBO = \angle 3 = 15^{\circ}$$.
- Тогда, $$\angle BOC = 180^{\circ} - 15^{\circ} - 15^{\circ}=150^{\circ}$$.
- Угол между диагоналями: $$\angle DOC = 180^{\circ}-150^{\circ}=30^{\circ}$$.
Радиус окружности, описанной около треугольника со сторонами $$4$$ см, $$6$$ см и $$8$$ см, больше радиуса вписанной в этот треугольник окружности:
- По формуле $$S = \sqrt{p(p-a)(p-b)(p-c)}$$, где $$p=\frac{a+b+c}{2}$$, найдём площадь треугольника:
$$S = \sqrt{9 \cdot 5 \cdot 3 \cdot 1} = 3 \sqrt{15}$$ (см$$^2$$).
- По формуле $$R=\frac{abc}{4S}$$ получим:
$$R=\frac{4 \cdot 6 \cdot 8}{4 \cdot 3\sqrt{15}}=\frac{16}{\sqrt{15}}$$ (см).
- По формуле $$r=\frac{2S}{a+b+c}$$ получим:
$$r=\frac{2 \cdot 3\sqrt{15}}{4+6+8}=\frac{\sqrt{15}}{3}$$ (см).
- $$\frac{R}{r}=\frac{16}{\sqrt{15}}\cdot \frac{3}{\sqrt{15}}=3,2$$.
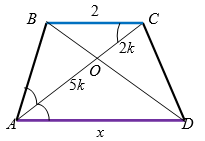
Диагонали трапеции точкой их пересечения делятся в отношении $$5 : 2$$. Если меньшее из оснований трапеции равно $$2$$, то ее большее основание равно:
Так как $$\triangle AOD \sim \triangle COB $$, то $$\frac{AO}{CO}=\frac{AD}{CB}$$,
откуда $$\frac{5k}{2k}=\frac{x}{2}$$, $$x=5=AD$$.
Модуль разности сумм вертикальных углов, изображенных на рисунке $$1$$, равен:
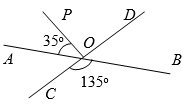
- $$\angle COB = \angle AOD = 135^\circ$$ (вертикальные углы).
- $$\angle DOB = \angle AOC = 180^\circ - 135^\circ = 45^\circ$$ (вертикальные углы).
- $$\left|(135^\circ+135^\circ)-(45^\circ+45^\circ) \right|=180^\circ$$.

Если один из внутренних углов правильного $$n$$-угольника на $$50$$ % больше внутреннего угла правильного треугольника, то сумма всех его внутренних углов равна:
- Внутренний угол правильного треугольника:
$$\alpha=\frac{180^\circ}{3}=60^\circ$$.
- Внутренний угол правильного $$n$$-угольника:
$$\beta=60^\circ +30^\circ = 90^\circ$$.
- По формуле $$\frac{180^\circ(n-2)}{n}=\beta$$ получим:
$$\frac{180^\circ(n-2)}{n}=90^\circ$$, $$2n-4=n$$, $$n=4$$.
- $$90^\circ \cdot 4 = 360^\circ$$.
Если меньшая диагональ правильного шестиугольника равна $$3\sqrt{3}$$ , то его периметр равен:
- По теореме косинусов (рис. $$3$$):
$$AB^2 = AC^2 + BC^2 -2AC \cdot BC \cdot \cos 120^{\circ}$$,
$$27 = a^2 + a^2 - 2a^2 \cdot (-0,5)$$,
$$27 = 3a^2$$, откуда $$a=3$$.
- $$P=6a=18$$.

Окружность, центр которой расположен на большей стороне треугольника, касается двух других его сторон. Если длины сторон треугольника равны $$5$$, $$10$$ и $$12$$, то центр окружности делит сторону треугольника на отрезки, модуль разности длин которых равен:
Так как $$BO$$ - биссектриса треугольника $$ABC$$ (рис. 7), то:
$$\frac{AB}{AO}=\frac{CB}{CO}$$, $$\frac{5}{x}=\frac{10}{12-x}$$, откуда $$x=4$$.
Тогда, $$CO-AO=8-4=4$$.
Если площадь квадрата равна $$\sqrt[3]{9}$$ , то его диагональ равна:
Так как $$S=\frac{d^2}{2}$$, то $$d^2 = 2\cdot \sqrt[3]{3^2}$$, откуда $$d=\sqrt{2} \cdot \sqrt[3]{3} = \sqrt[6]{72}$$.
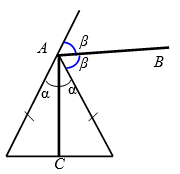
Биссектриса внешнего угла при вершине равнобедренного треугольника образует с медианой, проведенной к его основанию, угол, градусная мера которого равна:
$$\angle BAC = \alpha + \beta$$ (рис. 4).
Так как $$2 \alpha + 2\beta = 180^{\circ}$$, то $$\alpha + \beta = 90^{\circ}$$.