Планиметрия КТ 3
Количество острых углов, изображенных на рисунке $$1$$, равно:
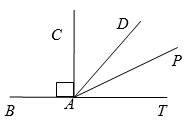
Острые углы: $$\angle CAD$$, $$\angle DAP$$, $$\angle PAT$$, $$\angle CAP$$, $$\angle DAT$$.

Если смежные стороны прямоугольника относятся как $$4 : 3$$, а его периметр равен $$28$$ м, то площадь прямоугольника равна:
- Так как $$2(4k+3k)=28$$, то $$k=2$$.
Тогда: $$a=8$$ м, $$b=6$$ м.
- $$S=ab=8 \cdot 6=48$$ (м$$^2$$).
Сходственные стороны подобных треугольников соответственно равны $$2$$ и $$6$$. Если площадь меньшего из них равна $$3$$, то площадь большего треугольника равна:
Так как $$a_1=2$$, $$a_2=6$$ и $$S_1=3$$, то $$\frac{S_1}{S_2}=\frac{a_1^{2}}{a_2^{2}}$$.
Получим: $$\frac{3}{S_2}=\frac{4}{36}$$, откуда $$S_2=27$$.В окружности радиуса $$5$$ проведены две параллельные хорды. Если длины этих хорд соответственно равны $$6$$ и $$8$$, то наименьшее расстояние между ними равно:
- Четырёхугольник $$ABCD$$ - равнобокая трапеция (рис. $$4$$), где $$KA=LD=1$$.
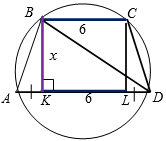
Рис. 4 - По теореме Пифагора:
$$AB=\sqrt{x^{2}+1}$$, а $$DB=\sqrt{x^{2}+49}$$.
- Рассмотрим треугольник $$ABD$$.
Найдём его площадь: $$S=\frac{1}{2}\cdot AD \cdot x = 4x$$.
По формуле $$R=\frac{abc}{4S}$$ получим:
$$5=\frac{\sqrt{x^{2}+1} \cdot \sqrt{x^{2}+49}\cdot 8}{4\cdot 4x}$$, $$10x=\sqrt{(x^{2}+1)(x^{2}+49)}$$,
$$x^{4}-50x^{2}+49=0$$, откуда $$x^2=1$$ или $$x^2=49$$.
Тогда, $$x_1=1$$, а $$x_2=7$$.
Если сумма длин больших диагоналей правильного шестиугольника равна $$6\sqrt{3}$$, то его площадь равна:
- Так как $$3d=6\sqrt{3}$$, а $$d=2a$$, то $$6a=6\sqrt{3}$$, откуда $$a=\sqrt{3}$$.
- По формуле $$S=\frac{6\sqrt{3}a^2}{4}$$ получим:
$$S=\frac{6\sqrt{3} \cdot 3}{4} = 4,5\sqrt{3}$$.
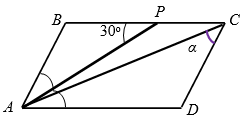
Биссектриса длины $$3\sqrt{3}$$ острого угла параллелограмма пересекает большую из его сторон под углом $$30^{\circ}$$. Если с большей диагональю она образует угол $$10^{\circ}$$, то эта диагональ с меньшей из сторон параллелограмма образует угол, градусная мера которого равна:
- На рисунке 3: $$\angle BAP = \angle DAP = \angle APB = 30^{\circ}$$.
- $$\angle CAD = 30^{\circ}-10^{\circ}=20^{\circ}$$.
- $$\angle B=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}=\angle D$$.
- $$\angle ACD = 180^{\circ}-20^{\circ}-120^{\circ}=40^{\circ}$$.
Отношение длин описанной около квадрата площадью $$4$$ окружности и вписанной в этот квадрат окружности равно:
- По формуле $$S=\frac{d^2}{2}$$ получим: $$4 = \frac{d^2}{2}$$, откуда $$d=2\sqrt{2}$$.
- По формуле $$S=a^2$$ получим: $$4=a^2$$, откуда $$a=2$$.
- Найдем радиус описанной окружности: $$R=\frac{d}{2}=\frac{2\sqrt{2}}{2}=\sqrt{2}$$.
Найдём длину описанной окружности: $$L=2\pi R = 2\sqrt{2} \pi$$.
- Найдем радиус вписанной окружности: $$r=\frac{a}{2}=\frac{2}{2}=1$$.
Найдём длину вписанной окружности: $$l=2\pi r= 2\pi$$.
- $$\frac{L}{l}=\frac{2\sqrt{2}\pi}{2\pi}=\sqrt{2}$$.
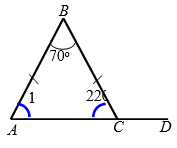
Если внутренний угол при вершине равнобедренного треугольника равен $$70^{\circ}$$ , то внешний угол при его основании равен:
- $$\angle 1 = \angle 2 = (180^{\circ}-70^{\circ}):2 = 55^{\circ}$$ (рис. 2).
- $$\angle BAC = 180^{\circ}-55^{\circ}=125^{\circ}$$.
Если площадь кругового сектора с центральным углом $$150^{\circ}$$ равна $$\frac{15\pi}{16}$$, то длина дуги, ограничивающей этот сектор, равна:
- По формуле $$S=\frac{\pi R^2}{360^{\circ}} \cdot n^{\circ}$$ получим:
$$\frac{15\pi}{16}=\frac{\pi R^2 \cdot 150^{\circ}}{360^{\circ}}$$, откуда $$R=1,5$$.
- По формуле $$l=\frac{2 \pi R}{360^{\circ}} \cdot n^{\circ}$$ получим:
$$l=\frac{2 \pi \cdot 1,5 \cdot 150^{\circ}}{360^\circ}= 1,25 \pi$$.
Если один из углов правильного $$n$$-угольника равен $$108^{\circ}$$, то сумма всех его внутренних углов (в градусах) равна:
По формуле $$\frac{180^{\circ}(n-2)}{n}=\beta$$ получим:
$$\frac{180^{\circ}(n-2)}{n}=108^{\circ}$$, $$45n-90=27n$$, $$n=5$$.
Тогда, $$108^{\circ} \cdot 5 = 540^{\circ}$$.

