Загрузка
ТестыСправкаQualiMe РегистрацияВход
ТестыСправкаQualiMe
РегистрацияВход
Тесты Школьник
Планиметрия КТ 6

Планиметрия КТ 6

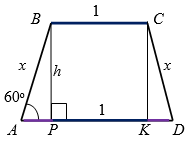
Если один из углов равнобедренной трапеции с меньшим основанием $$1$$ равен $$60^{\circ}$$, а её периметр равен $$5$$, то площадь трапеции равна:

  1. Так как $$\angle BAP = 60^{\circ}$$, то $$\angle ABP=30^{\circ}$$ (рис. $$5$$).

    Тогда, $$AP=\frac{1}{2}AB=0,5x$$.

    Следовательно, $$AD=0,5x+1+0,5x=x+1$$.

    2. Рис. 5
  2. Так как $$P=5$$, то $$(x+1)+x+1+x=5$$, откуда $$x=1$$, $$AD=2$$.
  3. Из теоремы Пифагора:

    $$h=\sqrt{AB^{2}-AP^{2}}$$, $$h=\sqrt{1-0,25}=0,5\sqrt{3}$$.

  4. По формуле $$S=\frac{(AD+BC) \cdot h}{2}$$ получим:

    $$S=\frac{(2+1)\cdot 0,5 \sqrt{3}}{2}=0,75\sqrt{3}$$.

Выберите один из вариантов

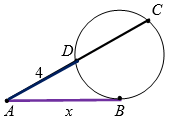
К окружности из одной точки проведены касательная и секущая так, что длина секущей в два раза больше длины касательной. Если внешний отрезок секущей равен $$4$$, то длина касательной равна:

Пусть $$AB=x$$, тогда $$AC=2x$$ (рис. $$4$$).

По свойству касательной и секущей:

$$AB^2=AC \cdot AD$$,

$$x^2=2x\cdot 4$$, откуда $$x=8$$.

Рис. 4

Выберите один из вариантов

Две окружности радиусов $$2$$ и $$6$$ касаются внутренним образом. Если через центр большей из них к меньшей окружности провести касательные, которые пересекут окружность в точках $$A$$ и $$B$$, то длина хорды $$AB$$ будет равна:

Так как $$OD=6$$ (рис. $$8$$), а $$PD=2$$, то $$OP=6-2=4$$.

Так как $$\triangle OKP \sim \triangle OTA$$, то:

$$\frac{KP}{TA}=\frac{OP}{OA}$$, $$\frac{2}{TA}=\frac{4}{6}$$, откуда $$TA=3$$.

Тогда, $$BA=6$$.

Рис. 8
Введите ответ в поле

Если стороны треугольника относятся как $$2 : 1,5 : 3$$, а его периметр равен $$26$$, то площадь треугольника равна:

  1. Так как $$2k+1,5k+3k=26$$, то $$k=4$$.

    Тогда: $$a=8$$, $$b=6$$, $$c=12$$.

  2. По формуле $$S=\sqrt{p(p-a)(p-b)(p-c)}$$:

    $$S=\sqrt{13(13-8)(13-6)(13-12)}=\sqrt{455}$$.

Выберите один из вариантов

Смежным с углом $$AOC$$ на рисунке $$1$$ является угол:

Рис. 1

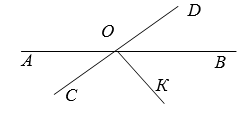
Угол $$AOD$$ и угол $$COB$$.

Выберите один из вариантов

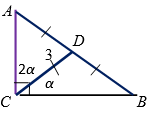
Если медиана, проведенная из прямого угла треугольника, равна $$3$$ и делит этот угол в отношении $$1 : 2$$, то меньший катет треугольника равен:

  1. Так как $$\alpha + 2\alpha=90^{\circ}$$, то $$\alpha = 30^{\circ}$$ (рис. $$3$$).
  2. По свойству медианы, проведенной к гипотенузе:

    $$DA=DB=CD=3$$.

  3. Треугольник $$ADC$$ – равносторонний, следовательно, $$AC=3$$.
Рис. 3

Введите ответ в поле

Если проекции катетов треугольника на гипотенузу равны $$12$$ и $$27$$, то произведение катетов равно:

  1. По свойству $$CD=\sqrt{AD \cdot BD}$$ (рис. $$7$$) получим:

    $$CD=\sqrt{12\cdot 27}=18$$.

    2. Рис. 7
  2. По теореме Пифагора:

    $$a=\sqrt{18^{2}+27^{2}}=9\sqrt{2^{2}+3^{2}}=9\sqrt{13}$$;

    $$b=\sqrt{18^{2}+12^{2}}=6\sqrt{3^{2}+2^{2}}=6\sqrt{13}$$.

  3. $$ab=9\sqrt{13} \cdot 6\sqrt{13}=702$$.

Введите ответ в поле

Если периметр параллелограмма равен $$3$$ дм, а разность его смежных сторон составляет $$1$$ см, то сумма квадратов его диагоналей равна:

  1. Так как $$P=2(a+b)$$, $$b=a+1$$, то $$30=2(2a+1)$$,

    откуда $$a=7$$ см, $$b=8$$ см.

  2. По формуле $$d_{1}^{2}+d_{2}^{2}=2a^{2}+2b^{2}$$ получим:

    $$d_{1}^{2}+d_{2}^{2}=98+128=226$$ (см$$^2$$).

Выберите один из вариантов

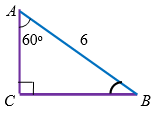
Если гипотенуза прямоугольного треугольника равна $$6$$, а острый угол треугольника равен $$60^{\circ}$$, то периметр этого треугольника равен:

  1. Так как $$\angle B = 30^{\circ}$$, то $$AC=6:2=3$$ (рис. $$2$$).
  2. Из теоремы Пифагора: $$CB=\sqrt{36-9}=3\sqrt{3}$$.
  3. $$P=3+6+3\sqrt{3}=9+3\sqrt{3}$$.
Рис. 2

Выберите один из вариантов

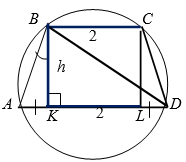
Высота равнобедренной трапеции равна $$\frac{3\sqrt{3}}{4}$$ и образует с ее боковой стороной угол $$60^{\circ}$$. Если меньшее основание трапеции равно $$2$$, то радиус окружности, описанной около трапеции, равен:

  1. Рассмотрим прямоугольный треугольник $$ABK$$ (рис. $$6$$).

    Так как $$\angle ABK=60^{\circ}$$, то $$\angle BAK = 30^{\circ}$$.

    Тогда, $$AB=2h=\frac{3\sqrt{3}}{2}$$

    Из теоремы Пифагора: $$AK = \sqrt{\frac{27}{4}-\frac{27}{16}}=\frac{9}{4}$$.

    2. Рис. 6
  2. Рассмотрим треугольник $$KBD$$.

    Так как $$LD=AK=\frac{9}{4}$$, то $$KD=2+\frac{9}{4}=\frac{17}{4}$$.

    По теореме Пифагора: $$BD=\sqrt{\frac{27}{16}+\frac{289}{16}}=\frac{\sqrt{79}}{2}$$.

  3. Рассмотрим треугольник $$ABD$$.

    Найдем его площадь:

    $$S=\frac{1}{2} \cdot AD \cdot h$$, $$S=\frac{1}{2} \cdot \frac{13}{2} \cdot \frac{3\sqrt{3}}{4}=\frac{39\sqrt{3}}{16}$$.

    По формуле $$R=\frac{abc}{4S}$$ получим:

    $$R=\frac{\frac{3\sqrt{3}}{2}\cdot \frac{\sqrt{79}}{2}\cdot \frac{13}{2}}{\frac{4 \cdot 39\sqrt{3}}{16}}=\frac{3\sqrt{3}}{2} \cdot \frac{\sqrt{79}}{2} \cdot \frac{13}{2} \cdot \frac{4}{39\sqrt{3}}=0,5\sqrt{79}$$.

Выберите один из вариантов
© Сиротина И.К., 2013—2024