Планиметрия КТ 7
В равнобедренный треугольник вписана окружность. Если точка касания делит боковую сторону треугольника на отрезки $$6$$ и $$4$$, то периметр треугольника равен:
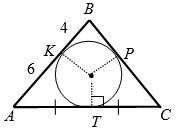
Случай 1. По свойству касательных (рис. 4):
$$BK=BP=6$$, $$AT=AK=4$$, $$CT=CP=4$$.
Тогда, $$P=2 \cdot (6+4+4)=28$$.
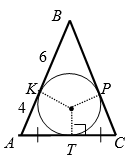
Случай 2. По свойству касательных (рис. 5):
$$BK=BP=4$$, $$AT=AK=6$$, $$CT=CP=6$$.
Тогда, $$P=2 \cdot (4+6+6)=32$$.
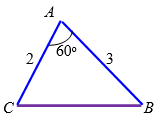
Если стороны треугольника, длины которых равны соответственно $$2$$ см и $$3$$ см, образуют угол $$60^{\circ}$$, то длина третьей стороны треугольника равна:
По теореме косинусов (рис. 2):
$$CB^2=AC^{2}+AB^{2}-2AC \cdot AB \cdot \cos 60^{\circ}$$,
$$CB^2=4+9-2 \cdot 2\cdot 3 \cdot \frac{1}{2}=7$$,
$$CB=\sqrt{7}$$ см.
Если один из углов треугольника в три раза меньше другого, а третий угол равен полусумме первых двух и площадь треугольника равна $$2\sqrt{3}$$, то большая сторона треугольника равна:
- Пусть $$\angle A = \alpha$$, $$\angle C=3\alpha$$, $$\angle B = (\alpha + 3\alpha):2=2\alpha$$ (рис. 6).
Получим: $$\alpha + 3\alpha +2\alpha=180^{\circ}$$, откуда $$\alpha = 30^{\circ}$$.
Тогда, $$\angle A = 30^{\circ}$$, $$\angle C=90^{\circ}$$, $$\angle B=60^{\circ}$$.
- Пусть $$AB=x$$. Тогда $$CB=2x$$ (по свойству катета, лежащего напротив угла $$30^{\circ}$$).
- По формуле $$S=\frac{1}{2} \cdot AB \cdot CB \cdot \sin 2\alpha$$ получим:
$$2\sqrt{3}=\frac{1}{2} \cdot x \cdot \frac{x}{2} \cdot \frac{\sqrt{3}}{2}$$, откуда $$x=4$$.

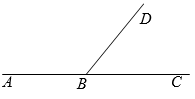
Если угол $$DBC$$ на $$30^{\circ}$$ меньше смежного с ним угла $$ABD$$, то градусная мера угла $$DBA$$ равна:
Пусть $$\angle DBA = x^{\circ}$$, тогда $$\angle DBC=x^{\circ}-30^{\circ}$$ (рис. $$1$$).
Получим: $$x+x-30=180$$, откуда $$x=105^{\circ}$$.
Если одна из диагоналей ромба равна $$3$$ мм и составляет $$120$$% от его второй диагонали, то сторона ромба равна:
- Так как $$d_1=3$$ мм, то $$d_2=\frac{3 \cdot 100}{120}=2,5$$ (мм).
- По формуле $$d_1^2+d_2^2=4a^2$$ получим:
$$4a^2=9+6,25$$, $$a^2=\frac{61}{16}$$, откуда $$a=0,25\sqrt{61}$$ (мм).
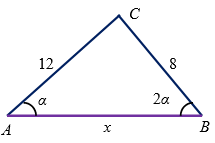
Если стороны разностороннего треугольника равны $$8$$ и $$12$$, а углы, лежащие против этих сторон относятся как $$1 : 2$$, то длина третьей стороны треугольника равна:
- По теореме синусов (рис. 8):
$$\frac{12}{\sin 2\alpha}=\frac{8}{\sin \alpha}$$, $$\frac{3}{2\sin \alpha \cos \alpha}=\frac{2}{\sin \alpha}$$, $$\frac{3}{2\cos \alpha}=\frac{2}{1}$$, $$\cos \alpha = \frac{3}{4}$$.
- По теореме косинусов (рис. 8):
$$64=x^2+144-24x \cdot \frac{3}{4}$$, $$x^2-18x+80=0$$,
откуда $$x_1 = 10$$, $$x_2=8$$ (посторонний корень).
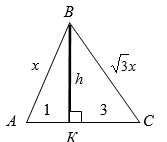
Если стороны треугольника относятся как $$1 : \sqrt{3}$$, а их проекции на третью сторону равны $$1$$ и $$3$$, то площадь треугольника равна:
- Из теоремы Пифагора (рис. 3):
$$h^2=x^{2}-1$$ и $$h^2=3x^{2}-9$$.
Тогда, $$x^2-1=3x^2-9$$, откуда $$x=2$$, $$h=\sqrt{3}$$.
- По формуле $$S=\frac{1}{2} \cdot AC \cdot BK$$ получим:
$$S=\frac{1}{2} \cdot 4 \cdot \sqrt{3}=2\sqrt{3}$$.
Если диаметр окружности равен $$\frac{1}{\sqrt{\pi}}$$, то длина окружности равна:
По формуле $$C=\pi \cdot d$$ получим:
$$C=\frac{\pi}{\sqrt{\pi}}=\sqrt{\pi}$$.
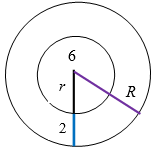
Если ширина кольца, образованного концентрическими окружностями, равна $$2$$, а его площадь равна $$8\pi$$, то радиус большей окружности равен:
Площадь кольца (рис. 9):
$$\pi R^2 - \pi r^2=8\pi$$, $$(R-r)(R+r)=8$$.
Так как $$R-r=2$$, то $$R+r=4$$.
Складывая уравнения $$R-r=2$$ и $$R+r=4$$, получим:
$$2R=6$$, откуда $$R=3$$.
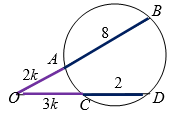
Хорды окружности, длины которых соответственно равны $$2$$ и $$8$$, продолжены до их взаимного пересечения. Если продолжения хорд относятся как $$2 : 3$$, то сумма длин их продолжений равна:
По свойству секущих (рис. $$7$$):
$$OB \cdot OA = OD \cdot OC$$,
$$(8+2k) \cdot 2k=(2+3k)\cdot 3k$$,
$$16+4k=6+9k$$, откуда $$k=2$$.
Тогда, $$OA+OC=5k=10$$.