Стереометрия КТ 2
Если пирамида имеет $$8$$ ребер, то отношение числа всех ее вершин к числу боковых граней равно:
Четырехугольная пирамида (рис. 1) имеет $$8$$ ребер:
$$SA$$, $$SB$$, $$SC$$, $$SD$$, $$AB$$, $$BC$$, $$CD$$, $$DA$$.
Вершины пирамиды: $$S$$, $$A$$, $$B$$, $$C$$, $$D$$.
Боковые грани: $$SAB$$, $$SBC$$, $$SCD$$, $$SDA$$.
Тогда, $$5:4=1,25$$.
В шар вписана прямая треугольная призма, в основании которой лежит прямоугольный треугольник с острым углом $$30^{\circ}$$, а наибольшая из ее боковых граней – квадрат. Если радиус шара равен $$\sqrt{6}$$, то объем призмы равен:
На рисунке 8: точка $$O$$ – центр шара, $$R$$ – радиус шара, грань $$AA_{1}C_{1}C$$ – квадрат.

По теореме Пифагора: $$x^2 + x^2 = 4R^2$$, $$x^2 = 2 \cdot 6$$, откуда $$x=2\sqrt{3}$$.
Так как $$\angle BAC = 30^{\circ}$$, то $$cos 30^{\circ} = \frac{AB}{x}$$, $$\frac{\sqrt{3}}{2}=\frac{AB}{2\sqrt{3}}$$, откуда $$AB=3$$.
Площадь основания призмы:
$$S=\frac{1}{2} AC \cdot AB \cdot sin 30^{\circ}$$, $$S=\frac{1}{2} \cdot 2\sqrt{3} \cdot 3 \cdot \frac{1}{2}=\frac{3\sqrt{3}}{2}$$.
Объем призмы: $$V=S \cdot AA_{1} = \frac{3\sqrt{3}}{2} \cdot 2\sqrt{3} = 9$$.
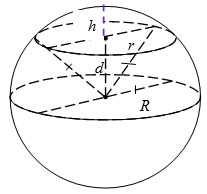
Площадь сечения шара некоторой плоскостью на $$80$$ % меньше площади сечения, проходящего через его диаметр. Если диаметр шара равен $$10$$, то это сечение удалено от центра шара на расстояние, равное:
-
Площадь сечения, проходящего через диаметр шара:
$$S_1 = \pi R^2 =25\pi$$.
- Площадь меньшего сечения: $$S_2 = 25\pi \cdot 0,2=5\pi$$.
Так как $$5\pi=\pi r^2$$, то $$r=\sqrt{5}$$.
-
Из теоремы Пифагора (рис. 5):
$$AO=\sqrt{R^2 - r^2}=\sqrt{25-5}=2 \sqrt{5}$$.

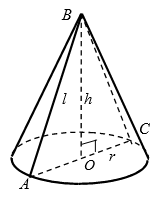
Если осевым сечением конуса является равносторонний треугольник со стороной $$1$$, то высота конуса относится к радиусу его основания как:
Так как $$l=2r$$, то $$h=\sqrt{4r^{2}-r^2}=\sqrt{3}r$$ (рис. 3).
Тогда, $$\frac{h}{r}=\frac{\sqrt{3}r}{r}=\frac{\sqrt{3}}{1}$$.
Если сфера, площадь поверхности которой равна $$4$$, вписана в цилиндр, то площадь поверхности цилиндра равна:
- Площадь сферы: $$S=4\pi R^2$$, $$4=4\pi R^2$$, откуда $$R=\frac{1}{\sqrt{\pi}}$$.
- Так как радиус цилиндра $$r=R=\frac{1}{\sqrt{\pi}}$$, а его образующая $$l=2R=\frac{2}{\sqrt{\pi}}$$, то площадь поверхности цилиндра равна:
$$S=2\pi R^2 +2\pi \cdot R \cdot 2R=6\pi R^2 = \frac{6\pi}{\pi}=6$$.
Если шар касается всех граней треугольной призмы с ребрами оснований $$4$$ см, $$4$$ см и $$2$$ см, то объем призмы равен:
-
Площадь основания призмы (рис. 2):
$$S=\sqrt{p(p-a)(p-b)(p-c)}$$, $$S=\sqrt{5\cdot 1 \cdot 1 \cdot 3} = \sqrt{15}$$ (см$$^2$$).
-
Радиус окружности, вписанной в основание призмы:
$$r=\frac{2S}{a+b+c}$$, $$r=\frac{2\sqrt{15}}{4+4+2}=\frac{\sqrt{15}}{5}$$ (см).
- Высота призмы: $$h=2r=\frac{2\sqrt{15}}{5}$$ (см).
- Объем призмы: $$V=S\cdot h$$, $$V=\sqrt{15} \cdot \frac{2\sqrt{15}}{5}=6$$ (см$$^3$$).

Боковое ребро правильной четырехугольной усеченной пирамиды равно $$\sqrt{11}$$ и наклонено к плоскости основания под углом, тангенс которого равен $$1,5\sqrt{2}$$. Если периметр меньшего основания пирамиды равен $$8$$, то ее объем равен:
-
Рассмотрим верхнее основание пирамиды (рис. 9).
Так как $$P=8$$, то $$a_1 = 2$$.
Но так как $$S_1 = \frac{d_{1}^2}{2}$$, то $$d_1 = 2\sqrt{2}$$, а $$NC=\sqrt{2}$$.
-
Рассмотрим треугольник $$PCD$$.
Так как $$tg \alpha = \frac{h}{PD}$$, то $$\frac{3\sqrt{2}}{2}=\frac{h}{PD}$$, $$PD=\frac{h\sqrt{2}}{3}$$.
По теореме Пифагора: $$h^2 + \frac{2h^2}{9}=11$$, откуда $$h=3$$.
Тогда, $$PD=\sqrt{2}$$.
- Рассмотрим нижнее основание пирамиды.
Так как $$OD = OP +PD = 2\sqrt{2}$$, то $$d_2 = 4\sqrt{2}$$, а $$S_2 = \frac{d_{2}^2}{2} = 16$$.
- По формуле $$V=\frac{1}{3}h(S_{1} + S_{2}+\sqrt{S_{1}S_{2}})$$ получим:
$$V=\frac{1}{3} \cdot 3 \cdot (4+16+\sqrt{4 \cdot 16}) = 28$$.

Сторона ромба, описанного около шара, равна $$24$$, а его острый угол составляет $$30^{\circ}$$. Если высота шарового сегмента, отсекаемого плоскостью ромба от шара, в $$6$$ раз меньше высоты ромба, то диаметр шара равен:
- Найдем площадь ромба: $$S=a^2sin 30^{\circ}=24^2 \cdot \frac{1}{2}=288$$.
С другой стороны, $$S=a \cdot 2r$$. Тогда, $$r=\frac{288}{48}=6$$ (рис. 7).
- Найдем высоту шарового сегмента: $$h=\frac{2r}{6}=2$$.
Тогда, $$d=R-h=R-2$$.
- По теореме Пифагора:
$$R^2 = r^2 + d^2$$, $$R^2=36+(R-2)^2$$, откуда $$2R=20=D$$.
Если большая диагональ правильной шестиугольной призмы равна $$2$$ и образует с плоскостью ее основания угол $$30^{\circ}$$, то поверхность призмы равна:
- Рассмотрим треугольник $$ACD$$ (рис. 4).
Так как $$\angle A = 30^{\circ}$$, то $$h=\frac{d}{2}=1$$.
Из теоремы Пифагора: $$AD=\sqrt{4-1}=\sqrt{3}$$.
Тогда, $$AO=\frac{\sqrt{3}}{2}=a$$.
-
Найдем площадь основания призмы:
$$S_{осн.}=\frac{6\sqrt{3}a^2}{4}$$, $$S_{осн.}=\frac{9\sqrt{3}}{8}$$.
Найдем боковую поверхность призмы:
$$S_{бок.} = P_{осн.} \cdot h$$, $$S_{бок.}=3\sqrt{3}$$.
Найдем поверхность призмы:
$$S=2S_{осн.}+S_{бок.}$$, $$S=\frac{9\sqrt{3}}{4}+3\sqrt{3}=5,25\sqrt{3}$$.
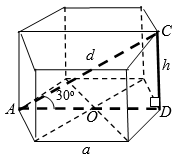
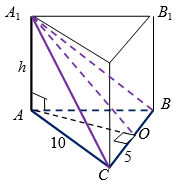
Если в основании прямой призмы лежит правильный треугольник со стороной $$10$$, а площадь сечения призмы, проходящего через одну из сторон нижнего основания и противолежащую ей вершину верхнего основания, равна $$5\sqrt{123}$$, то объем призмы равен:
-
Так как $$S_{сеч.}=\frac{CB \cdot A_{1}O}{2}$$ (рис. 6), то
$$5\sqrt{123}=\frac{10 \cdot A_{1}O}{2}$$, откуда $$A_{1}O= \sqrt{123}$$.
-
Из теоремы Пифагора:
$$AO=\sqrt{AC^2 - OC^2}=\sqrt{100-25}=\sqrt{75}$$;
$$A_{1}A=\sqrt{A_{1}O^2 - AO^2}=\sqrt{123-75}=4\sqrt{3}=h$$.
-
Объем призмы:
$$V = S_{осн.} \cdot h$$, $$V=\frac{CB \cdot AO}{2} \cdot h$$, $$V=\frac{10 \cdot 5\sqrt{3} \cdot 4\sqrt{3}}{2}=300$$.