Загрузка
ТестыСправкаQualiMe РегистрацияВход
ТестыСправкаQualiMe
РегистрацияВход
Тесты Школьник
Стереометрия КТ 4

Стереометрия КТ 4

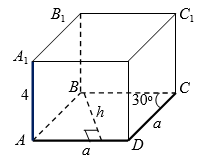
Высота прямого параллелепипеда равна $$4$$, а смежные стороны его основания образуют угол $$150^{\circ}$$. Если в параллелепипед можно вписать шар, то площадь поверхности параллелепипеда равна:

  1. Радиус шара: $$R=\frac{H}{2}=\frac{4}{2}=2$$ (рис. 3).
    2. Рис. 3
  2. Основание параллелепипеда ромб $$ABCD$$.

    Высота ромба: $$h=2R=4$$.

    Площадь ромба: $$S_{p}=a^2 sin 30^{\circ}=ah$$, $$\frac{1}{2}a^2 = 4a$$, откуда $$a=8$$.

    Тогда, $$S_{p}=4 \cdot 8=32$$.

  3. Площадь поверхности параллелепипеда:

    $$S=2S_{p} + 4a \cdot H =64+128=192$$.

Выберите один из вариантов

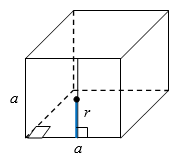
Если радиус окружности, вписанной в грань куба, равен $$\sqrt{6}$$, то площадь поверхности куба равна:

Так как $$a=2r$$, то $$a=2\sqrt{6}$$ (рис. 1).

Тогда, $$S=6a^2 = 6 \cdot 24 = 144$$.

Рис. 1
Выберите один из вариантов

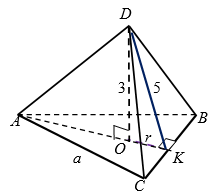
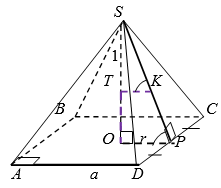
Если высота правильной треугольной пирамиды равна $$3$$, а апофема равна $$5$$, то боковая поверхность пирамиды равна:

  1. Из теоремы Пифагора (рис. 4):

    $$OK=\sqrt{25-9}=4=r$$.

    2. Рис. 4
  2. По формуле $$r=\frac{a}{2\sqrt{3}}$$ получим:

    $$4=\frac{a}{2\sqrt{3}}$$, откуда $$a=8\sqrt{3}$$.

  3. Найдем боковую поверхность пирамиды:

    $$S=\frac{1}{2}\cdot 3a \cdot DK=\frac{24\sqrt{3} \cdot 5}{2}=60\sqrt{3}$$.

Выберите один из вариантов

Расстояния между боковыми ребрами наклонной треугольной призмы равны $$2$$, $$3$$ и $$4$$. Если боковое ребро призмы равно $$1,6\sqrt{15}$$, то объем призмы равен:

  1. По формуле $$S=\sqrt{p(p-a)(p-b)(p-c)}$$, где $$p=\frac{a+b+c}{2}$$, найдём площадь сечения:

    $$S=\sqrt{\frac{9}{2} \cdot \frac{5}{2} \cdot \frac{3}{2} \cdot \frac{1}{2}}=\frac{3\sqrt{15}}{4}$$ (рис. 8).

  2. По формуле $$V=S \cdot l$$ получим:

    $$V=\frac{3\sqrt{15}}{4} \cdot \frac{8\sqrt{15}}{5}=18$$.

Рис. 8
Введите ответ в поле

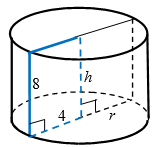
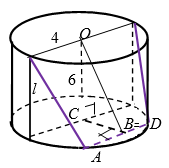
Через хорду длины $$4$$ нижнего основания цилиндра и диаметр длины $$8$$ его верхнего основания проходит сечение. Если образующая цилиндра равна $$6$$, то секущая плоскость наклонена к плоскости основания цилиндра под углом, градусная мера которого равна:

Так как $$CA=r=4$$ (рис.7), а $$AB=\frac{1}{2}AD=2$$,

то $$CB=\sqrt{16-4}=2\sqrt{3}$$.

Тогда, $$tg \angle OBC = \frac{OC}{CB}=\frac{6}{2\sqrt{3}}=\sqrt{3}$$, откуда $$\angle OBC = 60^{\circ}$$.

Рис. 7
Введите ответ в поле

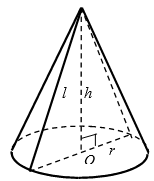
Если площадь боковой поверхности конуса, высота которого равна $$3\sqrt{3}$$, в два раза больше площади его основания, то объем конуса равен:

  1. Площадь поверхности конуса: $$S=\pi r^2 + \pi r l$$.

    Площадь основания конуса: $$S=\pi r^2$$.

    Так как $$\pi r^2 +\pi r l=2\pi r^2$$, то $$l=2r$$.

  2. По теореме Пифагора (рис. 5):

    $$4r^2 = r^2 + h^2$$, откуда $$r=\frac{h}{\sqrt{3}}=\frac{3\sqrt{3}}{3}=3$$.

  3. Объем конуса:

    $$V=\frac{1}{3}\pi r^2 h$$, $$V=\frac{\pi \cdot 9 \cdot 3\sqrt{3}}{3}=9\sqrt{3} \pi$$.

Рис. 5
Выберите один из вариантов

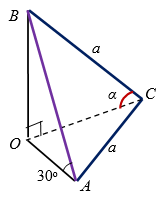
Если гипотенуза равнобедренного прямоугольного треугольника, один из катетов которого принадлежит плоскости $$\alpha$$, образует с этой плоскостью угол $$30^{\circ}$$, то другой катет треугольника образует с этой плоскостью угол (в градусах), равный:

  1. Так как $$\angle ACB =90^{\circ}$$ (рис. 10), то $$AB=\sqrt{a^2 + a^2}=\sqrt{2}a$$.
  2. Тогда, $$OB=\frac{AB}{2}=\frac{\sqrt{2}a}{2}$$.
  3. Так как $$sin \alpha =\frac{OB}{a}=\frac{\sqrt{2}a}{2a}=\frac{\sqrt{2}}{2}$$, то $$\alpha = 45^{\circ}$$.
Рис. 10
Введите ответ в поле

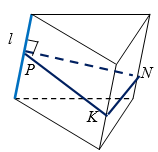
В правильную четырехугольную пирамиду, боковые грани которой наклонены к плоскости основания под углом $$30^{\circ}$$, вписан цилиндр так, что его верхнее основание находится на расстоянии $$1$$ см от вершины пирамиды. Если площадь основания пирамиды равна $$108$$ см$$^2$$, то объем цилиндра равен:

  1. Рассмотри пирамиду с ребром основания $$a$$ (рис. 6).

    Так как $$a^2=108$$, то $$a=6\sqrt{3}$$ см. Тогда, $$OP=r=3\sqrt{3}$$ см.

    Так как $$\angle SPO = 30^{\circ}$$, а $$tg 30^{\circ}=\frac{SO}{PO}$$, то

    $$\frac{1}{\sqrt{3}}=\frac{SO}{3\sqrt{3}}$$, откуда $$SO=3$$ см.

    2. Рис. 6
  2. Рассмотрим цилиндр.

    Так как $$ST=1$$ см, то $$TO=3-1=2=H$$.

    Так как $$\angle SKT =30^{\circ}$$, то $$tg 30^{\circ}=\frac{ST}{TK}$$, $$\frac{1}{\sqrt{3}}=\frac{1}{TK}$$, откуда $$TK=\sqrt{3}=R$$.

    Найдем объем цилиндра: $$V=\pi R^2 H=6\pi$$ (см$$^3$$).

Выберите один из вариантов

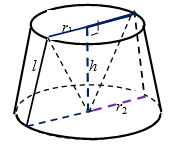
Радиус основания усеченного конуса и его высота равны $$5$$. Если объем полного конуса, основанием которого является меньшее из оснований усеченного конуса, а вершина находится в центре большего основания, в $$7$$ раз меньше объема усеченного, то радиус большего основания усеченного конуса равен:

  1. Объем полного конуса (рис. 9):

    $$V=\frac{\pi r_{1}^2 h}{3}=\frac{\pi \cdot 25 \cdot 5}{3}=\frac{125\pi}{3}$$.

  2. Объем усеченного конуса:

    $$V=\frac{1}{3} \pi h(r_{1}^2 +r_{2}^2 +r_{1}r_{2})$$, $$V=\frac{5\pi}{3} \cdot (25 + r_{2}^2 + 5r_{2})$$.

  3. Так как $$7 \cdot \frac{125\pi}{3}=\frac{5\pi}{3} \cdot (25 + r_{2}^2 + 5r_{2})$$,

    то $$r_{2}^2 +5r_{2}-150 = 0$$, откуда $$r_{2}=10$$.

Рис. 9
Введите ответ в поле

Прямоугольник со смежными сторонами $$4$$ и $$8$$ вращается вокруг его большей стороны. Боковая поверхность тела вращения равна:

Тело вращения: цилиндр (рис. 2).

Тогда, $$S=2\pi r l$$, $$S=2\pi \cdot 4 \cdot 8 = 64\pi$$.

Рис. 2
Выберите один из вариантов
© Сиротина И.К., 2013—2024