Алгебраические функции ИТ
На множестве всех действительных чисел определены функции:
1) $$y=\sqrt[3]{x+1}$$;
2) $$y=\sqrt{x+1}$$;
3) $$y=\left | x \right |+\left |2-x \right |$$;
4) $$y=\frac{x}{2+x}$$;
5) $$y=x^{2}+5x-1$$.
- Область определения функции $$D(f)$$ – множество всех допустимых значений переменной $$x$$.
- Множество всех действительных чисел обозначают $$R$$.
Запишем области определений данных функций:
1) $$y=\sqrt[3]{x+1}$$, $$D(f): x\in R$$;
2) $$y=\sqrt{x+1}$$, $$D(f): x\geq -1$$;
3) $$y=\left | x \right |+\left |2-x \right |$$, $$D(f): x\in R$$;
4) $$y=\frac{x}{2+x}$$, $$D(f): x\in R/x\neq -2$$;
5) $$y=x^{2}+5x-1$$, $$D(f): x\in R$$.
На множестве всех действительных чисел определены функции $$1, 3$$ и $$5$$.
Находя область определения выражения, необходимо задавать себе вопрос: "При каком значении $$x$$ оно лишено смысла (нельзя найти значение этого выражения)?" Если таких чисел не найдется, то записать $$x\in R$$, а если найдутся, то исключить их из множества $$R$$.
Графики функций $$f_{1}(x)=x^{3}+2x$$ и $$f_{2}(x)=-2x^{2}-1$$ пересекаются в точке:
Если точка $$A(x_{0};y_{0})$$ принадлежит графику функции $$y=f(x)$$ , то справедливо равенство $$y_{0}=f(x_{0})$$ .
Подставим координаты точек в каждое из уравнений:
1) рассмотрим точку $$A(1;-3)$$ :
$$ 1+2\neq -3$$, поскольку точка $$A$$ не принадлежит графику первой функции, то не имеет смысла проверять ее принадлежность графику второй функции;
2) рассмотрим точку $$B(5;3)$$ :
$$125+10\neq 3$$;
3) рассмотрим точку $$C(0;0)$$ :
$$0+0=0$$, но $$0-1\neq 0$$;
4) рассмотрим точку $$D(-1;-3)$$ :
$$-1-2=-3$$ и $$-2-1=-3$$;
5) рассмотрим точку $$E(1;-6)$$ :
$$1+2\neq -6$$.
Графики функций пересекаются в точке $$D(-1;-3)$$ .
- Если точка не принадлежит графику первой функции, то мы не проверяем ее принадлежность второму графику.
- Точку пересечения графиков функций $$y=f_{1}(x)$$ и $$y=f_{2}(x)$$ можно найти, решая систему уравнений: $$\left\{\begin{matrix} y=f_{1}(x) , & \\ y=f_{2}(x). & \end{matrix}\right.$$
Число решений системы равно числу точек пересечения линий. Если же система решений не имеет, то линии не пересекаются.
Однако в нашем случае этот способ решения не рациональный, так как могут возникнуть затруднения с решением уравнения $$x^{3}+2x=-2x^{2}-1$$.
Разность наибольшего целого числа из промежутка убывания и наименьшего целого числа из промежутка возрастания функции $$y=x^{2}+5x-2$$ равна:
- Функцию вида $$y=ax^{2}+bx+c$$, где $$a,b,c$$ – действительные числа $$(a\neq 0)$$, называют квадратичной.
- Графиком функции является парабола.
- Если $$a> 0$$, то ветви параболы направлены вверх, а если $$a<0$$, то – вниз.
- Координаты вершины параболы находят по формулам:
$$x_{0}=\frac{-b}{2a}$$, $$y_{0}=f(x_{0})$$. - Прямая $$x_{0}=\frac{-b}{2a}$$ – ось симметрии параболы.
Координаты вершины параболы в нашем случае находить не обязательно.
Если парабола проходит через точки $$A(1;2)$$ и $$B(-1;0)$$, а прямая $$x=0,5$$ – ось ее симметрии, то сумма координат вершины параболы, увеличенная в $$8$$ раз, равна:
Если точка $$A(x_{0};y_{0})$$ принадлежит графику функции $$y=f(x)$$, то справедливо равенство $$y_{0}=f(x_{0})$$.
Укажите выражения, которые являются функциями:
1) $$5x-10y=8$$;
2) $$xy=-5$$;
3) $$\left | x \right |+ \left | y \right |=6$$;
4) $$y^{2}=x^{2}-1$$;
5) $$y=\sqrt{1+x^{2}}$$.
Функцией $$y=f(x)$$ называют такую зависимость переменной $$y$$ от переменной $$x$$, при которой каждому допустимому значению $$x$$ соответствует единственное значение $$y$$. При этом переменную $$x$$ называют независимой переменной или аргументом функции, а переменную $$y$$ – зависимой от $$x$$ переменной или значением функции.
Выразим явно $$y$$ в каждом из равенств:
- $$5x-10y=8$$, $$10y=5x-8$$, $$y=0,5x-0,8$$.
- $$xy=-5$$, $$y=\frac{-5}{x}$$ (где $$x\neq 0$$ ).
- $$\left | x \right |+\left | y \right |=6$$, $$\left | y \right |=6-\left | x \right |$$, $$y=\pm (6-\left | x \right |)$$, (где $$6-\left | x \right |\geq 0$$ ).
- $$y^{2}=x^{2}-1$$, $$y=\pm \sqrt{x^{2}-1}$$ (где $$x^{2}\geq 1$$ ).
- $$y=\sqrt{1+x^{2}}$$.
Так как каждому значению $$x$$ соответствует единственное значение $$y$$, то это выражение является функцией. Например, пусть $$x=2$$, тогда $$y=0,5\cdot 2-0,8=0,2$$.
Так как каждому значению $$x$$ cоответствует единственное значение $$y$$, то это выражение является функцией. Например, пусть $$x=1$$, тогда $$y=-5$$.
Например, пусть $$x=3$$, тогда $$y=\pm 3$$ и выражение $$\left | x \right |+\left | y \right |=6$$ не является функцией.
Например, пусть $$x=4$$, тогда $$y=\pm \sqrt{15}$$ и выражение $$y^{2}=x^{2}-1$$ не является функцией.
Так как каждому значению $$x$$ соответствует единственное значение $$y$$, то это выражение является функцией. Например, пусть $$x=0$$, тогда $$y=1$$.
Выразить явно $$y$$ в равенстве $$f(x,y)=0$$ это значит, записать это равенство в виде $$y=f(x)$$.
Уравнение окружности с центром в точке $$P(3;-1)$$ и радиусом равным $$4$$ имеет вид:
- Если уравнение окружности имеет вид $$x^{2}+y^{2}=R^{2}$$,
то ее центр находится в точке $$O(0;0)$$, а радиус равен $$R$$. - Если уравнение окружности имеет вид $$(x-a)^{2}+(y-b)^{2}=R^{2},$$ то ее центр находится в точке $$O{}'(a;b)$$, а радиус равен $$R$$.
Так как $$a=3$$, $$b=-1$$, а $$R=4$$, то запишем:
$$(x-3)^{2}+(y+1)^{2}=16$$.
Уравнение окружности можно записать иначе:
$$\left | x-a \right |^{2}+\left | y-b \right |^{2}=R^{2}$$.
Нечетными являются функции:
1) $$f(x)$$$$=\left | 5-x \right |$$;
2) $$f(x) = x-2x^{2}+12$$;
3) $$f(x)= -25x$$;
4) $$f(x)=\frac{4x^{4}}{x^{2}+2}$$;
5) $$f(x)=\sqrt{2+x}$$.
Множество действительных чисел $$R$$ симметричное.
Уравнение квадрата с центром в точке $$P(-3;0)$$ и диагональю равной $$4$$ имеет вид:
- Если уравнение квадрата имеет вид $$\left | x \right |+\left | y \right |=\frac{d}{2}$$, то точка $$O(0;0)$$ – точка пересечения диагоналей квадрата, а $$d$$ – длина его диагонали.
- Если уравнение квадрата имеет вид $$\left | x -a\right |+\left | y -b\right |=\frac{d}{2}$$, то точка $$O{}'(a;b)$$ – точка пересечения диагоналей квадрата, а $$d$$ – длина его диагонали.
Так как $$a=-3$$, $$b=0$$, а $$d=4$$, то запишем:
$$\left | x+3 \right |+\left | y \right |=2$$.
Различайте:
1) $$\left | x-a \right |^{2}+\left | y-b \right |^{2}=R^{2}$$– уравнение окружности;
2) $$\left | x-a \right |+\left | y-b \right |=\frac{d}{2}$$– уравнение квадрата.
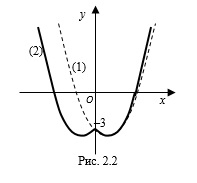
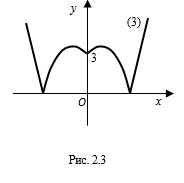
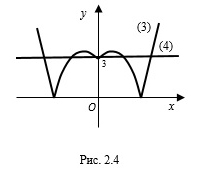
Количество точек пересечения графиков функций $$y=\left | x^{2} -2 \left |x \right |-3 \right |$$ и $$y=3$$ равно:
- Построение графика функции $$y=f(\left |x \right |)$$: часть графика функции $$y=f(x)$$ правее оси $$Oy$$ оставляем и ее же отражаем симметрично этой оси.
- Построение графика функции $$y=\left |f(x) \right |$$: часть графика функции $$y=f(x)$$ над осью $$Ox$$ оставляем, а ту, что под осью, отражаем симметрично этой оси.
- Теорема Виета: если имеем приведенное квадратное уравнение вида $$x^{2}+px+q=0$$, то сумма корней этого уравнения равна коэффициенту при переменной $$x$$, записанному с противоположным знаком, а произведение его корней равно свободному члену уравнения: $$x_{1}+x_{2}=-p, x_{1}\cdot x_{2}=q$$.
- Координаты вершины параболы $$y=ax^2+bx+c$$ находят по формулам: $$x_{0}=\frac{-b}{2a}, y_{0}=f(x_{0})$$.
Если некоторая прямая проходит через точку $$M(2;-2)$$ и параллельна прямой $$2x+4y=7$$, то ее уравнение имеет вид:
- Линейной называют функцию вида $$y=kx+b$$, где $$k$$ и $$b$$ – некоторые действительные числа. График линейной функции – прямая. Число $$k$$ – угловой коэффициент этой прямой.
- Прямые $$y=k_{1}x+b_{1}$$ и $$y=k_{2}x+b_{2}$$ параллельны, если $$k_{1}=k_{2}$$ и $$b_{1}\neq b_{2}$$.
Если точка $$A(x_{0};y_{0})$$ принадлежит графику функции $$y=f(x)$$, то справедливо равенство $$y_{0}=f(x_{0})$$.