Исследование функции с помощью производной ИТ
Количество точек экстремума функции $$y=(1-x^3)^2$$ равно:

- Точки экстремума функции необходимо искать среди нулей производной функции.
- Не всякий нуль производной функции является точкой ее экстремума
Произведение наибольшего отрицательного и наименьшего положительного чисел из промежутков возрастания функции $$y=\frac{1}{x}+\frac{x}{4}$$ равно:
Достаточное условие возрастания функции: если на заданном промежутке $$f'(x)> 0$$, то функция $$y=f(x)$$ возрастает на этом промежутке.

$$x=0$$ – двукратный корень уравнения $$4x^{2}=0$$.
Наименьшее значение функции $$y=3+3x^2-x^3$$ на отрезке $$[-1; 1]$$ равно:
Алгоритм нахождения наибольшего и наименьшего значений функции $$y=f(x)$$ на заданном отрезке:
1) находим $$f'(x)$$;
2) находим нули производной функции, решая уравнение $$f'(x)=0$$;
3) находим значение функции на концах отрезка и в нулях производной, принадлежащих данному отрезку;
4) определяем наибольшее и наименьшее значение из полученных.
- Точка $$x=2$$ не принадлежит заданному отрезку.
- Свое наибольшее или наименьшее значение функция может принимать только либо на концах отрезка, либо в нулях производной, принадлежащих этому отрезку.
Функция $$f(x)=x\sqrt[3]{x}+2lg2$$ убывает на промежутке:
Поскольку $$2lg2$$ – число, то $$(2lg2)'=0$$.
Если $$n$$ – количество нулей функции $$y=(3-2x)^2-4$$, а $$m$$ – количество нулей ее производной, то сумма чисел $$n$$ и $$m$$ равна:
Формула сокращенного умножения:
$$(a-b)^2=a^2-2ab+b^2$$.- Нули функции $$y=f(x)$$ находят, решая уравнение $$f(x)=0$$.
- Нули производной функции $$y=f(x)$$ находят, решая уравнение $$f'(x)=0$$.
Если разность двух целых чисел равна 8, то наименьшее из произведений этих чисел равно:

Находя точки экстремума, мы определяем на промежутках знаки производной функции, а не самой функции.
Разность наибольшего и наименьшего значений функции $$y=2x\sqrt{x}+5x$$ на отрезке $$[1; 4]$$ равна:
Алгоритм нахождения наибольшего и наименьшего значений функции $$y=f(x)$$ на заданном отрезке:
1) находим $$f'(x)$$;
2) находим нули производной функции, решая уравнение $$f'(x)=0$$;
3) находим значение функции на концах отрезка и в нулях производной, принадлежащих данному отрезку;
4) определяем наибольшее и наименьшее значение из полученных.
Если функция не имеет нулей производной, то наибольшее и наименьшее значения она принимает на концах заданного отрезка.
Точками минимума функции $$f(x)=x^4-0, 5x^2+2$$ являются точки:
Алгоритм определения точек экстремума функции $$y=f(x)$$:
1) находим $$f'(x)$$;
2) находим нули производной функции, решая уравнение $$f'(x)=0$$;
3) наносим нули производной на $$D(f)$$ функции;
4) определяем знак производной на полученных промежутках;
5) определяем точки экстремума по правилу: если при переходе через свой нуль производная меняет знак c «+» на «–», то имеем точку максимума, а если с «–» на «+» – точку минимума.

Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы функции могут оказаться больше ее максимумов. Функция может иметь несколько минимумов и максимумов.
Если в правильный треугольник со стороной 8 вписать параллелограмм, имеющий общий угол с треугольником, то периметр параллелограмма наибольшей площади будет равен:
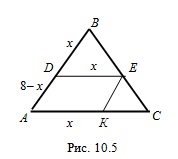

Ромбом называют параллелограмм, у которого все стороны равны.
Функция $$y=\frac{2+x}{\sqrt{x}}$$ не убывает, если:
Различайте записи:
$$(ax)'=a(x)'=a\cdot 1=a$$ ; $$(a+x)'=a'+x'=0+1=1$$.
