Функции КТ 3
Графики функций $$ \sqrt[3]{x-7}$$ и $$3y-2x=-15$$ пересекаются в точке:
Подставим координаты точек в каждое из уравнений:
- $$-2\neq \sqrt[3]{1-7}$$, $$-6-2\neq -15$$;
- $$3\neq \sqrt[3]{5-7}$$, $$9-10\neq -15$$;
- $$-1=\sqrt[3]{6-7}$$, $$-3-12=-15$$;
- $$6\neq \sqrt[3]{-1-7}$$, $$18+2\neq -15$$;
- $$-6\neq \sqrt[3]{1-7}$$, $$-18-2\neq -15$$;
Если система уравнений $$\begin{cases} y+2x+1=b,\\ ay+3a=x \end{cases} $$ имеет бесконечно много решений, то произведение чисел $$a$$ и $$b$$ равно:
Система уравнений имеет бесконечное множество решений, если прямые $$ y=-2x+b-1$$ и $$ y=\frac{1}{a}\cdot x-3$$ совпадают.
Следовательно, $$ \frac{1}{a}=-2$$, а $$ b-1=-3$$.
Тогда: $$ a=-0,5$$; $$ b=-2$$; $$ ab=1$$.
Произведение наименьшего числа из области определения и наибольшего из области значений функции $$ y=1-\sqrt{x+5}$$ равно:
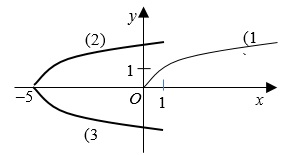
- Построим график функции $$ y=\sqrt{x}$$ ($$1$$) (рис. $$2$$).
- Построим график функции $$ y=\sqrt{x+5}$$ ($$2$$):
выполним параллельный перенос графика ($$1$$) вдоль оси $$Ox$$ на $$5$$ единичных отрезков влево (рис. $$2$$). -
Построим график функции $$ y=-\sqrt{x+5}$$ ($$3$$):
отражаем график ($$2$$) симметрично относительно оси $$Ox$$ (рис. $$2$$). -
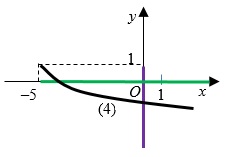
Построим график функции $$ y=1-\sqrt{x+5}$$ ($$4$$):
выполним параллельный перенос графика ($$3$$) вдоль оси $$Oy$$ на $$1$$ единичный отрезок вверх (рис. $$3$$). - Тогда: $$ x_{наим.}=-5$$; $$ y_{наиб.}=1$$; $$ -5\cdot 1=-5$$.
Количество корней уравнения $$ 2^{x}+5^{x}=1$$ равно:
Запишем уравнение в виде: $$ 2^{x}=1-5^{x}$$.
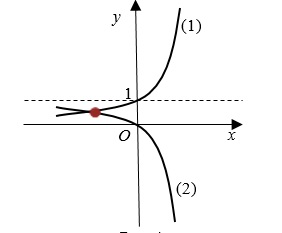
Построим графики функций $$ f\left ( x \right )=2^{x}$$ ($$1$$) и $$ f\left ( x \right )=1-5^{x}$$ ($$2$$).
Так как графики функций имеют одну точку пересечения (рис. $$4$$), то уравнение имеет один корень.
Если прямая проходит через точки $$ A\left ( 1;2 \right )$$ и $$ B\left ( -3;-1 \right )$$, то ее уравнение имеет вид:
$$\begin{cases} k+b=2,\\ -3k+b=-1; \end{cases} \begin{cases} k+b=2,\\ 4k=3;\end{cases} \begin{cases} b=1,25,\\ k=0,75. \end{cases}$$
Уравнение прямой: $$ y=0,75x+1,25$$.
Отрицательные на всей своей области определения функции:
- $$y=-3^{x}$$;
- $$ y=log_{2}\left ( -x \right )$$;
- $$ y=arcsinx $$;
- $$ y=arctgx $$;
- $$ y=sin\left ( -x \right ) $$.
Запишем области значений данных функций:
- $$y=-3^{x}$$, $$E\left ( f \right ):y< 0$$;
- $$ y=log_{2}\left ( -x \right )$$, $$ E\left ( f \right ):y\in R$$;
- $$ y=arcsinx $$, $$ E\left ( f \right ):y\in \left \lfloor -0,5\pi ; 0,5\pi \right \rfloor $$;
- $$ y=arcctgx $$, $$ E\left ( f \right ):y\in \left ( 0;\pi \right ) $$;
- $$ y=sin\left ( -x \right ) $$, $$ E\left ( f \right ):y\in \left [ -1;1 \right ]$$.
Количество нулей функции $$ f\left ( x \right )=\left ( cos2x+sin2x \right )^{2}$$ на отрезке $$ \left [ 0;2\pi \right ]$$ равно:
- $$f\left ( x \right )cos^{2}2x+sin^{2}2x+2cos2xsin2x$$, $$f\left ( x \right )=1+sin4x$$.
-
$$1+sin4x=0 $$, $$sin4x=-1 $$, откуда
$$4x=-\frac{\pi }{2}+2\pi n$$, $$x=-\frac{\pi }{8}+\frac{\pi n}{2}$$, где $$n\in Z$$. - Нули функции на отрезке $$ \left [ 0;2\pi \right ]$$:
если $$n=1$$, то $$ x=\frac{3\pi }{8}$$; если $$n=2$$, то $$ x=\frac{7\pi }{8}$$;
если $$n=3$$, то $$ x=\frac{11\pi }{8}$$; если $$n=4$$, то $$ x=\frac{15\pi }{8}$$.
Количество целых чисел, принадлежащих промежутку, на котором определена функция, обратная к функции $$y=sinx$$, равно:
Функция $$y=arcsinx$$ определена на промежутке $$ \left [ -0,5\pi ;0,5\pi \right ]$$.
Целые числа: $$-1$$; $$0$$; $$1$$.
Периодическими являются функции:
- $$y=sinx$$;
- $$y=tgx$$;
- $$ y=arcctgx $$;
- $$ y=arccosx $$;
- $$ y=arcsinx $$;
- Функция $$ y=sinx $$ периодическая, наименьший период равен $$ 2\pi $$.
- Функция $$y=tgx$$ периодическая, наименьший период равен $$\pi$$.
- Функция $$ y=arcctgx $$ непериодическая.
- Функция $$ y=arccosx $$ непериодическая.
- Функция $$ y=arcsinx $$ непериодическая.
Среднее арифметическое всех целых значений функции $$ y=\left | x \right |$$ на промежутке $$ \left ( -5;2,5 \right ]$$ равно:
Согласно рисунку $$1$$ запишем:
$$\left ( 0+1+2+3+4 \right ):5=2$$.


