Вариационные ряды ИТ
Дан интервальный вариационный ряд:
Гистограмма относительных частот имеет вид:
Гистограммой относительных частот выборки называют столбчатую диаграмму, состоящую из прямоугольников, основаниями которых являются длины интервалов, которые содержат значения вариант, высотами – относительные частоты интервалов.
На координатной плоскости (рис. 1.7) построим прямоугольники, основаниям которых являются промежутки $$[1;4)$$, $$[4;7)$$, $$[7;10)$$, $$[10;13]$$, а высотами являются отрезки соответственно длин: $$0,2$$; $$0,3$$; $$0,1$$; $$0,4$$.
Гистограммой частот выборки называют столбчатую диаграмму, состоящую из прямоугольников, основаниями которых являются длины интервалов, которые содержат значения вариант, высотами – частоты данных интервалов.
Полигон частот и относительных частот строят для дискретного вариационного ряда.
Гистограмму частот и относительных частот строят для интервального вариационного ряда.
Дан дискретный вариационный ряд:
Медиана равна:
Медиана дискретного вариационного ряда:
$$m_{e}=\frac{1}{2}\left ( a_{\frac{n}{2}}+a_{\frac{n}{2}+1} \right )$$,
где $$n$$ – объем выборки и $$n$$ четное число.
Так как $$n=10$$, то
$$m_{e}=\frac{1}{2}\left ( a_{5} + a_{6}\right )$$,
$$m_{e}=\frac{5, 2+6, 4}{2}=5,8$$.
$$a_{5}=5, 2$$ – значение варианты с порядковым номером $$5$$,
$$a_{6}=6, 4$$ – значение варианты с порядковым номером $$6$$.
Даны значения признака $$X$$:
$$10$$ ; $$4$$; $$5$$; $$2$$; $$4$$; $$5$$; $$6$$; $$4$$; $$8$$; $$2$$; $$10$$.
Медиана равна:
Медиана $$m_{e}$$ – значение параметра, относительно которого статистическая совокупность делится на две равные части.
Медиана дискретного вариационного ряда:
$$m_{e}=a_{\frac{n+1}{2}}$$,
где $$n$$ – объем выборки и $$n$$ нечетное число.
Расположим значения признака в порядке возрастания:
$$2$$; $$2$$; $$4$$; $$4$$; $$4$$; $$5$$; $$5$$; $$6$$; $$8$$; $$10$$; $$10$$.
Так как $$n=11$$, то $$m_{e}=a_{\frac{11+1}{2}}=a_{6}=5$$.
Чтобы найти медиану дискретного вариационного ряда, варианты необходимо расположить в порядке возрастания.
Рассмотрим выборку $$CBX$$ $$x_{1}, x_{2}, . . . , x_{n}$$ объема $$n$$.
Чтобы построить дискретный вариационный ряд, необходимо:
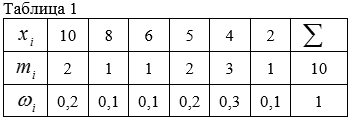
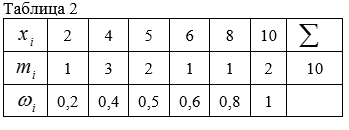
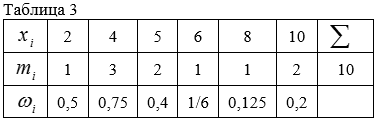
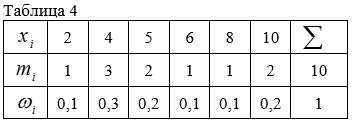
1) расположить значения признака $$X$$ (варианты) в порядке возрастания: $$x_{1} < x_{2} < x_{3} < ... < x_{k}$$;
2) найти частоты $$m_{i}$$ вариант;
3) найти относительные частоты $$w_{i}=\frac{m_{i}}{n}$$ вариант.
$$\sum_{i=1}^{k}m_{i}=n$$, где $$n$$ – объем выборки;
$$\sum_{i=1}^{k}\omega_{i}=1$$.
Дан интервальный вариационный ряд:
Мода равна:
Моду интервального вариационного ряда находят по формуле:
$$m_{0}=x_{i}+\frac{h(m_{i}-m_{i-1})}{2m_{i}-m_{i-1}-m_{i+1}}$$,
где $$(x_{i}; x_{i+1})$$ – модальный интервал, т. е. интервал, которому соответствует наибольшая частота $$m_{i}$$;
$$h$$ – длина модального интервала.
Модальный интервал: $$[7; 10)$$.
Тогда: $$x_{i}=7$$, $$m_{i}=6$$, $$m_{i-1}=3$$, $$m_{i+1}=5$$, $$h=10-7=3$$.
Мода: $$m_{0}=7+\frac{3\cdot (6-3)}{12-3-5}=9,25$$.
$$m_{i-1}$$ – частота предмодального интервала,
$$m_{i+1}$$ – частота послемодального интервала.
Чтобы построить интервальный вариационный ряд, необходимо:
1) найти размах вариации: $$R=x_{max}-x_{min}$$;
2) определить количество интервалов: $$k$$;
3) найти длину интервала: $$h=\frac{R}{k}$$;
4) найти частоты вариант на интервалах: $$m_{i}$$;
5) найти относительные частоты вариант на интервалах: $$w_{i}=\frac{m_{i}}{n}$$.
$$x_{1}=x_{min},$$ $$x_{k}=x_{max}$$.
Дан дискретный вариационный ряд:
Полигон частот имеет вид:
Полигоном частот выборки называют ломаную линию, соединяющую на координатной плоскости точки вида: $$(x_{i};m_{i})$$.
На координатной плоскости построим точки:
$$(0; 2)$$, $$(2; 4)$$, $$(4; 1)$$, $$(6; 8)$$, $$(8; 5)$$, $$(10; 6)$$.
Соединим построенные точки ломаной линией (рис. 1. 1).
Полигоном относительных частот выборки называют ломаную линию, соединяющую на координатной плоскости точки вида: $$(x_{i};w_{i})$$.
Дан дискретный вариационный ряд:
Эмпирическая функция распределения имеет вид:
Эмпирической функцией распределения выборки называют функцию вида:
$$F_{n}(x)=\left\{ \begin{array}{lcl} 0, & x\leq x_{1};\\w_{1}, & x_{1}< x \leq x_{2};\\w_{1}+w_{2}, & x_{2}< x \leq x_{3};\\ ... \\ 1, & x>x_{k}.\\ \end{array} \right.$$
Найдем накопленные относительные частоты:
Построим эмпирическую функцию распределения $$CBX$$ (рис. 1.12).
Эмпирическая функция распределения $$CBX$$ имеет вид:
$$F_{n}(x)=\left\{ \begin{array}{lcl} 0; & x< 2; \\ 0, 2; & 2< x \leq 4; \\ 0,5; & 4< x \leq 6; \\ 0,7; & 6< x \leq 8; \\ 0,8; & 8< x \leq 10;\\ 1; & x>10.\\ \end{array} \right.$$
Дан интервальный вариационный ряд:
Медиана равна:
Медиану интервального вариационного ряда находят по формуле:
$$m_{e}=x_{i}+\frac{h}{m_{i}}\left ( \frac{n}{2}-\sum_{j=1}^{i-1}m_{j} \right )$$,
где $$(x_{i}; x_{i+1})$$ – медианный интервал, т. е. первый интервал, накопленная частота которого превышает или равна половине общей суммы абсолютных частот;
$$h$$ – длина медианного интервала;
$$m_{i}$$ – частота медианного интервала;
$$\sum_{j=1}^{i-1}m_{j}$$ – накопленная частота предмедианного интервала;
$$n$$ – объем выборки.
Найдем накопленные частоты:
Если объем выборки равен $$n$$, то накопленная частота на последнем интервале также равна $$n$$:
