Транспортные задачи ИТ
Решите транспортную задачу (в таблице указаны тарифы перевозок):

- Модель ТЗ называется открытой, если суммарный запас груза у поставщиков не равен суммарному спросу потребителей.
- Если $$\sum_{i=1}^{m}a_i> \sum_{j=1}^{n}b_j$$, то необходимо ввести фиктивного потребителя $$B_{n+1}$$, потребность в грузе которого составит:
$$b_{n+1}=\sum_{i=1}^{m}a_i-\sum_{j=1}^{n}b_j$$. - Все тарифы перевозок от поставщиков к фиктивному потребителю будут равны нулю.

- План перевозок:
$$X^{*}=\begin{pmatrix} 70 &0 \\ 0 &110 \\ 80 & 0 \end{pmatrix}$$. - У поставщиков $$A_2$$ и $$A_3$$ останется по $$20$$ ед. груза.
- Стоимость перевозок:
$$f(X^{*})=70 \cdot 4+110 \cdot 2+80 \cdot5 = 900$$ (ден. ед.).
В процессе решения ТЗ открытую модель всегда необходимо преобразовывать в закрытую.
- $$A=\begin{bmatrix} 25 & 45 \end{bmatrix}$$;
$$B=\begin{bmatrix} 20 & 35& 15 \end{bmatrix}$$;
$$C^T=\begin{bmatrix} 5 & 7 & 2\\ 4 & 8 & 6 \end{bmatrix}$$;
$$X=\begin{bmatrix} 0 &20 \\ 10 &25 \\ 15 & 0 \end{bmatrix}$$.
- Целевая функция:
$$minf(X)=c_{11}x_{11}+c_{12}x_{12}+. . . +c_{1n}x_{1n}+. . . +c_{m1}x_{m1}+. . . +c_{mn}x_{mn}$$. - Система ограничений:
$$\sum_{j=1}^{n}x_{ij}=\sum_{i=1}^{m}a_i$$, $$\sum_{i=1}^{m}x_{ij}=\sum_{j=1}^{n}b_j$$, $$x_{ij}\geq 0$$ ($$i=\overline{1, m}$$ ; $$j=\overline{1, n}$$).
Распределительная таблица:

- Целевая функция:
$$minf(X)=5x_{11}+4x_{12}+7x_{21}+8x_{22}+2x_{31}+6x_{32}$$. - Система ограничений:
$$\sum_{j=1}^{2}x_{ij}=70$$, $$\sum_{i=1}^{3}x_{ij}=70$$, $$x_{ij}\geq 0$$ ($$i=\overline{1,3}$$; $$j=\overline{1,2}$$.
Модель ТЗ называется закрытой, если суммарный запас груза у поставщиков равен суммарному спросу потребителей.
Решите транспортную задачу (в таблице указаны тарифы перевозок):
- Если $$\sum_{i=1}^{m}a_i< \sum_{j=1}^{n}b_j$$, то необходимо ввести фиктивного поставщика $$A_{m+1}$$.
- Запас груза у фиктивного поставщика составит $$a_{m+1}=\sum_{j=1}^{n}b_j-\sum_{i=1}^{m}a_i$$.
- Все тарифы перевозок от фиктивного поставщика к потребителям будут равны нулю.
- План перевозок:
$$X^{*}=\begin{pmatrix} 35 &0&10 \\ 0 &50&5 \\ 0& 0& 65 \end{pmatrix}$$. - Потребитель$$B_1$$ не получит $$35$$ ед. груза.
- Стоимость перевозок:
$$f(X^{*})=35 \cdot 9+10 \cdot 8+50 \cdot 3+5 \cdot +65 \cdot 6=960$$ (ден. ед.).
- Все тарифы перевозок от поставщиков к фиктивному потребителю равны нулю.
- Все тарифы перевозок от фиктивного поставщика к потребителям также равны нулю.
Найдите оптимальный план перевозок и оптимальное значение целевой функции ТЗ:
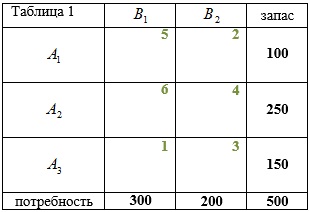
- Критерий оптимальности опорного плана: если все оценки свободных клеток неотрицательные, то план оптимальный.
- Правило «минимального элемента»:
1) выбираем клетку с минимальным тарифом и записываем в нее максимально возможное значение поставки;
2) из рассмотрения исключаем поставщика (и соответствующую ему строку), запасы которого исчерпаны, или потребителя (и соответствующий ему столбец), запросы которого полностью удовлетворены;
3) из оставшихся клеток снова выбираем клетку с наименьшим тарифом и записываем в нее максимально возможное значение поставки и т. д. - Сумма потенциалов загруженной клетки ($$i; j$$) равна ее тарифу:
$$c_{ij}=u_i+v_j$$. - Чтобы найти оценку свободной клетки ($$i; j$$), необходимо из тарифа клетки вычесть сумму ее потенциалов:
$$\Delta _{ij}=c_{ij}-(u_i+v_j)$$.
- По правилу «минимального элемента» найдем опорный план задачи (Таблица 2):
$$x_{31}=min(150; 300)=150$$ , $$x_{32}=0$$;
$$x_{12}=min(100; 200)=100$$ , $$x_{11}=0$$;
$$x_{22}=min(250; 100)=100$$, $$x_{21}=150$$.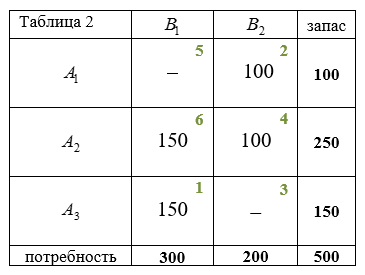
- Найдем потенциалы поставщиков и потребителей (Таблица 3).
Полагая $$u_1=0$$, получим:$$v_2=2-0=2$$, $$u_2=4-2=2$$, $$v_1=6-2=4$$, $$u_3=1-4=-3$$.
- Найдем оценки свободных клеток (Таблица 3):
$$\Delta _{11}=5-(4+0)=1$$, $$\Delta _{32}=3-(2-3)=4$$.
Так как оценки свободных клеток неотрицательные, то план оптимальный.

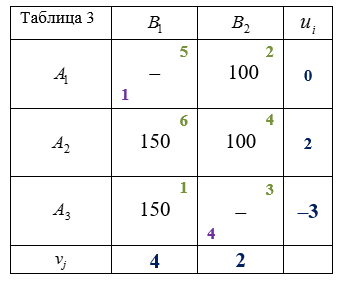
$$f(X^{*})=100 \cdot 2+150 \cdot 6+100 \cdot 4+150 \cdot 1= 1650$$ (ден. ед.).
Модель ТЗ называется закрытой, если суммарный запас груза у поставщиков равен суммарному спросу потребителей.
Найдите оптимальный план перевозок и оптимальное значение целевой функции ТЗ:

- Критерий оптимальности опорного плана: если все оценки свободных клеток неотрицательные, то план оптимальный.
- Если среди оценок окажутся отрицательные, то клетку, которой соответствует наименьшая отрицательная оценка, называют перспективной.
- План перевозок можно улучшить, перераспределяя максимально возможное количество груза по циклу, который образует перспективная клетка с другими загруженными клетками.
Пояснения к Таблице 2
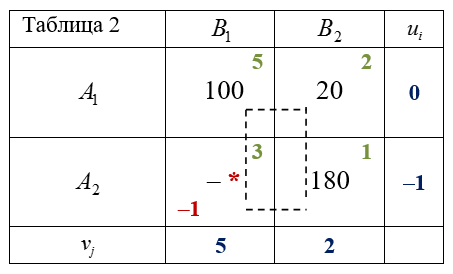
- Опорный план задачи:
$$x_{22}=min(180; 200)=180$$ , $$x_{21}=0$$ ;
$$x_{12}=min(120; 20)=20$$ , $$x_{11}=100$$ .
- Потенциалы:
$$u_1=0$$ , $$v_1=5-0=5$$ , $$v_2=2-0=2$$ , $$u_2=1-2=-1$$ .
- Оценки:
$$\Delta _{21}=3-(5-1)=-1< 0$$ .
План не оптимальный.
Клетка ($$2; 1$$) перспективная. Она образует цикл с клетками ($$1; 1$$), ($$1; 2$$) и ($$2; 2$$). Перемещая по циклу $$100$$ ед. груза, получим новый план перевозок, представленный в таблице 3.
Пояснения к Таблице 3
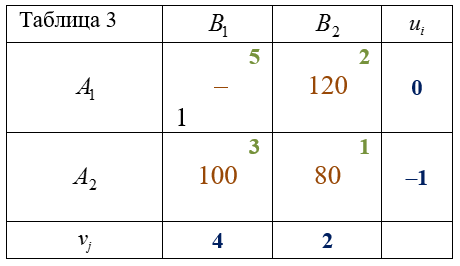
- Потенциалы:
$$u_1=0$$ , $$v_2=2-0=2$$ , $$u_2=1-2=-1$$ , $$v_1=3+1=4$$ .
- Оценки:
$$\Delta _{11}=5-(4+0)=1> 0$$ .
План оптимальный.


$$f(X^{*})=120 \cdot 2+100 \cdot 3+80 \cdot 1=620$$ (ден. ед.).
Перераспределение груза (Рисунок 10.9):

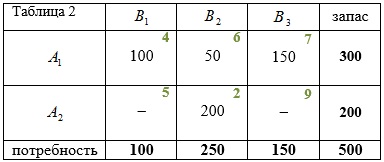
Найдите опорный план перевозок транспортной задачи по правилу «минимального элемента»:

- 1) выбираем клетку с минимальным тарифом и записываем в нее максимально возможное значение поставки;
2) из рассмотрения исключаем поставщика (и соответствующую ему строку), запасы которого исчерпаны, или потребителя (и соответствующий ему столбец), запросы которого полностью удовлетворены;
3) из оставшихся клеток снова выбираем клетку с наименьшим тарифом и записываем в нее максимально возможное значение поставки и т. д.
- Наименьшие затраты на перевозку (2 ден. ед.) соответствуют маршруту $$A_2-B_2$$, поэтому $$x_{22}=min(200;250)=200$$, следовательно, $$x_{21}=0$$, $$x_{23}=0$$, а соответствующие клетки таблицы свободны.
- Из оставшихся тарифов наименьший (4 ден. ед.) соответствует маршруту $$A_1-B_1$$, поэтому $$x_{11}=min(300;100)=100$$.
- Следующим рассматриваем маршрут $$A_1-B_2$$, следовательно, $$x_{12}=min(200;50)=50$$. Тогда, $$x_{13}=150$$.
- План перевозок: $$X=\begin{pmatrix} 100 & 50 &150 \\ 0 & 200 & 0 \end{pmatrix}$$.
Для того чтобы ТЗ имела допустимые планы, необходимо и достаточно выполнение равенства: $$\sum_{i=1}^{m}a_i=\sum_{j=1}^{n}b_j$.
Найдите оценки свободных клеток ТЗ:

- Чтобы найти оценку свободной клетки ($$i; j$$), необходимо из тарифа клетки вычесть сумму ее потенциалов:
$$\Delta _{ij}=c_{ij}-(u_i+v_j)$$. - Сумма потенциалов загруженной клетки ($$i; j$$) равна ее тарифу:
$$c _{ij}=u_i+v_j$$.
- Найдем потенциалы поставщиков и потребителей.
Зная, что $$v_3=0$$, получим:
$$u_1=c_{13}-v_3=7-0=7$$, $$v_1=4-7=-3$$, $$v_2=6-7=-1$$, $$u_2=2-(-1)=3$$. - Найдем оценки свободных клеток:$$\Delta _{21}=5-(-3+3)=5$$, $$\Delta _{23}=9-(0+3)=6$$.

Оценки загруженных клеток всегда равны нулю.
Найдите оптимальный план перевозок и оптимальное значение целевой функции ТЗ:

- Опорный план задачи должен содержать $$m+n-1$$ загруженных клеток, где $$m$$ – количество поставщиков, $$n$$ – количество потребителей.
- В случае, когда из распределительной таблицы одновременно исключается строка и столбец, в одну из свободных клеток записывают число $$0$$ и такую клетку условно считают загруженной (нуль-загрузка).
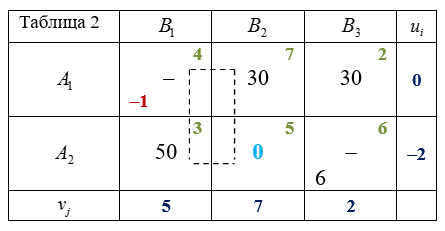
- Опорный план задачи:
$$x_{13}=min(60; 30)=30$$ , $$x_{23}=0$$ ;
$$x_{21}=min(50; 50)=50$$ , $$x_{11}=0$$ ,
$$x_{22}=0$$ , $$x_{12}=30$$ .Опорный план должен содержать $$m+n-1=2+3-1=4$$ загруженных клеток. В одну их свободных клеток запишем число $$0$$. Например, пусть $$x_{22}=0$$ .
- Потенциалы:
$$u_1=0$$ , $$v_2=7-0=7$$ , $$v_3=2-0=2$$ , $$u_2=5+2=7$$ , $$v_1=3+2=5$$ .
- Оценки:
$$\Delta _{11}=4-(5+0)=-1$$ ,
$$\Delta _{23}=6-(2-2)=6$$ .
План не оптимальный.
Перемещая по циклу $$30$$ ед. груза, получим новый план перевозок, представленный в таблице 3.

- Потенциалы:
$$u_1=0$$ , $$v_1=4-0=4$$ , $$v_3=2-0=2$$ , $$u_2=3-4=-1$$ , $$v_2=5+1=6$$ .
- Оценки:
$$\Delta _{12}=7-(6+0)=1$$ ,
$$\Delta _{23}=6-(2-1)=5$$ .
План оптимальный.
$$f(X^{*}=30 \cdot 4+30 \cdot 2+20 \cdot 3+30 \cdot 5=390$$ (ден. ед.).
Перераспределение груза (Рисунок 10.10):

Найдите потенциалы поставщиков и потребителей:
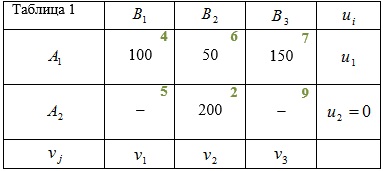
- $$c_{ij}=u_i+v_j$$.
- Так как $$u_2=0$$, то $$v_2=c_{22}-u_2=2-0=2$$.
- Тогда, $$u_1=6-2=4$$, $$v_1=4-4=0$$, $$v_3=7-4=3$$.
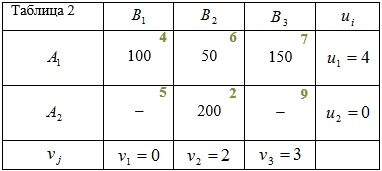
Чтобы найти потенциалы поставщиков и потребителей, необходимо один из потенциалов считать известным. В нашем случае мы положили, что $$u_2=0$$.
Известны матрицы транспортной задачи:
$$A=\begin{bmatrix} 25 & 45 \end{bmatrix}$$; $$B=\begin{bmatrix} 20 & 35& 15 \end{bmatrix}$$; $$C=\begin{bmatrix} 5 &7 &2 \\ 4 &8 & 6 \end{bmatrix}$$.

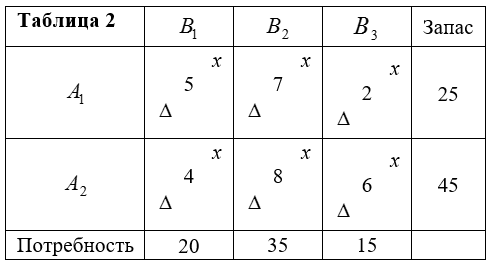


- Матрица запаса груза:
$$A=\begin{bmatrix} a_1 & a_2 & ... & a_m \end{bmatrix}$$ ;
- Матрица потребности в грузе:
$$B=\begin{bmatrix} b_1 & b_2 & ... & b_n \end{bmatrix}$$ ;
- Матрица тарифов перевозок:
$$C=\begin{bmatrix} c_{11} & c_{12} & ... &c_{1n} \\ c_{21} & c_{22} &... & c_{2n}\\ ... & ...& ... &... \\ c_{m1} & c_{m2} &... & c_{mn} \end{bmatrix}$$ ;
- Матрица перевозок:
$$X=\begin{bmatrix} x_{11} & x_{12} & ... &x_{1n} \\ x_{21} & x_{22} &... & x_{2n}\\ ... & ...& ... &... \\ x_{m1} & x_{m2} &... & x_{mn} \end{bmatrix}$$ .
Распределительная таблица ТЗ ( $$\Delta _{ij}$$ – оценки клеток):

Распределительная таблица ТЗ:


