Уравнения КТ 13
Произведение корней уравнения $$\sqrt{2x^2 - 3x + 2} = 2x^2 - 3x$$ равно:
Пусть $$\sqrt{2x^2 - 3x + 2} = a$$.
Тогда: $$2x^2 - 3x + 2 = a^2$$, $$2x^2 - 3x = a^2 - 2$$.
Получим: $$a^2 - a - 2 = 0$$, откуда $$D = 1$$, $$a_1 = -1$$, $$a_2 = 2$$.
Решим уравнение:
$$\sqrt{2x^2 - 3x + 2} = 2$$, $$2x^2 - 3x - 2 = 0$$,
откуда $$x_1x_2 = \frac{-2}{2} = -1$$, так как $$D > 0$$.
Абсолютная величина наибольшего отрицательного корня уравнения $$3sin2x = \sqrt{3}cos2x$$ равна:
-
$$tg2x = \frac{\sqrt{3}}{3}$$, $$2x = \frac{\pi}{6} + \pi n$$, $$x = \frac{\pi}{12} + \frac{\pi n}{2}$$, где $$n \in Z$$.
-
При $$n = -1$$ получим: $$x = -\frac{5\pi}{12}$$.
Тогда, $$\left|-\frac{5\pi}{12}\right| = \frac{5\pi}{12}$$.
Наименьший положительный корень (в градусах) уравнения $$sin2x + 4(cosx - sinx) = 4$$ равен:
-
Полагая $$sin2x = a$$, а $$cosx - sinx = b$$, получим:
$$a + 4b = 4$$, откуда $$a = 4 - 4b$$.
-
Выполним преобразования:
$$(cosx - sinx)^2 = b^2$$,
$$cos^2x + sin^2x - 2cosxsinx = b^2$$,
$$1 - a = b^2$$, откуда $$a = 1 - b^2$$.
-
Решим уравнение:
$$4 - 4b = 1 - b^2$$, $$b^2 - 4b + 3 = 0$$,
откуда $$b = 1$$ или $$b = 3$$ (посторонний корень).
-
Так как $$a = 0$$, то $$sin2x = 0$$, $$x = \frac{\pi n}{2}$$, $$n \in Z$$.
-
При $$n = 1$$ получим: $$90^{\circ}$$.
Наименьший целый корень уравнения $$log_{x - 1}(x^2 - 2x + 1) = 2$$ равен:
ОДЗ: $$x > 1$$ и $$x \neq 2$$.
$$log_{x - 1}(x - 1)^2 = 2$$, $$log_{x - 1}(x - 1) = 1$$, $$x - 1 = x - 1$$,
следовательно, $$x \in$$ ОДЗ.
Сумма всех действительных корней (или корень, если он единственный) уравнения $$2 \cdot 2^{2x} + 3 \cdot 2^x - 2 = 0$$ равна:
Полагая $$2^x = a > 0$$, получим:
$$2a^2 + 3a - 2 = 0$$,
откуда $$D = 25$$, $$a_1 = -2 < 0$$, $$a_2 = \frac{1}{2}$$.
Тогда, $$2^x = 2^{-1}$$, откуда $$x = -1$$.
Увеличенная в $$0,5$$ раза сумма корней уравнения $$lg(5x - 19)^2 = 0$$ равна:
ОДЗ: $$5x - 19 \neq 0$$.
$$(5x - 19)^2 = 10^0$$, откуда $$5x - 19 = 1$$ или $$5x - 19 = -1$$.
Следовательно, $$x = 4$$ или $$x = 3,6$$.
Тогда, $$0,5(4 + 3,6) = 3,8$$.
Среднее арифметическое всех целых значений $$a$$, при которых уравнение $$x^2 - 6|x| + 8 = a$$ имеет четыре решения, равно:
-
Построим параболу $$y = x^2 - 6x + 8$$ (1) (рис. 1).
Координаты вершины:
$$x_0 = \frac{-b}{2a} = 3$$, $$y_0 = 9 - 18 + 8 = -1$$.
Нули функции: $$x_1 = 2$$, $$x_2 = 4$$.
-
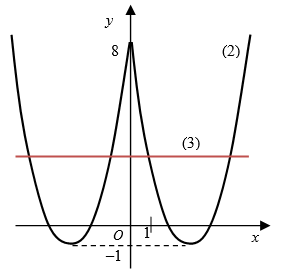
Построим график функции $$y = |x|^2 - 6|x| + 8$$ (2): часть графика (1), расположенного правее оси Оy, оставляем и ее же отражаем симметрично этой оси (рис. 2).
-
Построим прямую $$y = a$$ (3) так, чтобы она пересекала график (2) в четырех точках (рис. 2). Очевидно, что $$-1 < a < 8$$.
Тогда, $$(0 + 1 + 2 + 3 + 4 + 5 + 6 + 7) : 8 = 3,5$$.

Число, обратное модулю разности корней уравнения $$|6x - 7| = |x - 2|$$, равно:
$$(6x - 7)^2 = (x - 2)^2$$, $$(5x - 5)(7x - 9) = 0$$,
откуда $$x = 1$$ или $$x = \frac{9}{7}$$.
Тогда, $$\left|1 - \frac{9}{7}\right|^{-1} = 3,5$$.
Среднее арифметическое всех действительных корней уравнения $$x^3 + 3x^2 - 5x = 0$$ равно:
Запишем уравнение в виде:
$$x(x^2 + 3x - 5) = 0$$, откуда
$$x_1 = 0$$ или $$x^2 + 3x - 5 = 0$$.
Так как $$D = 9 + 20 = 29 > 0$$, то $$x_2 + x_3 = -3$$.
Тогда, $$\frac{x_1 + x_2 + x_3}{3} = \frac{0 - 3}{3} = -1$$.
Если $$(x; y)$$ – решение системы уравнений $$\left\{\begin{array}{l} \sqrt{\frac{y}{x}} - 2\sqrt{\frac{x}{y}} = 1, \\ \sqrt{5x + y} + \sqrt{5x - y} = 4, \end{array}\right.$$ то значение $$yx^{-1}$$ равно:
-
Рассмотрим первое уравнение системы.
Полагая $$\sqrt{\frac{y}{x}} = a > 0$$, получим:
$$a - \frac{2}{a} = 1$$, $$a^2 - a - 2 = 0$$,
откуда $$a_1 = 2$$, $$a_2 = -1 < 0$$.
Тогда: $$\sqrt{\frac{y}{x}} = 2$$, откуда $$y = 4x$$.
-
Рассмотрим второе уравнение системы.
$$\sqrt{5x + 4x} + \sqrt{5x - 4x} = 4$$,
$$3\sqrt{x} + \sqrt{x} = 4$$, $$4\sqrt{x} = 4$$, $$x = 1$$.
Тогда, $$y = 4$$.
-
$$yx^{-1} = 4 \cdot 1 = 4$$.

