Стереометрия КТ 6
Основание пирамиды – треугольник с катетами 6 и 8, а две ее боковые грани перпендикулярны плоскости основания и образуют двугранный угол, равный $$90^{\circ}$$. Если площадь наибольшей боковой грани пирамиды равна $$3\sqrt{89}$$, то ее высота равна:
- Рассмотрим основание пирамиды (рис. 7).
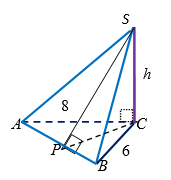
Рис.7 По теореме Пифагора: $$AB = \sqrt{64 + 36} = 10$$.
Так как $$S_{ABC} = \frac{1}{2} \cdot CA \cdot CB = \frac{1}{2} \cdot AB \cdot CP$$,
то $$8 \cdot 6 = 10 \cdot CP$$, откуда $$CP = 4,8$$. - Так как $$S_{ABC} = \frac{1}{2} \cdot AB \cdot SP = 3\sqrt{89}$$, то
$$\frac{1}{2} \cdot 10 \cdot SP = 3\sqrt{89}$$, откуда $$SP = \frac{3\sqrt{89}}{5}$$.
- Из теоремы Пифагора:
$$h = \sqrt{SP^2 - PC^2} = \sqrt{\frac{801}{25} - \frac{576}{25}} = 3$$.
Если в конус, боковой поверхностью которого является сектор с центральным углом $$216^{\circ}$$ и радиусом $$5$$, вписан шар, то площадь поверхности шара равна:
- Длина дуги сектора: $$L = \frac{2\pi \cdot 5 \cdot 216^{\circ}}{360^{\circ}} = 6\pi$$.
- Длина окружности основания конуса: $$C = 2\pi r$$.
Так как $$C = L = 6\pi$$, то $$r = 3$$ (рис. 4).
Из теоремы Пифагора: $$h = \sqrt{l^2 - r^2} = \sqrt{25 - 9} = 4$$.
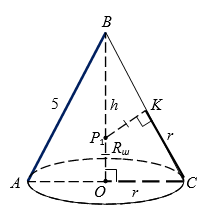
Рис.4 - Так как $$\bigtriangleup BOC \sim \bigtriangleup BKP$$, то $$\frac{BO}{BK} = \frac{OC}{KP}$$.
Получим: $$\frac{4}{5-3} = \frac{3}{R}$$, откуда $$R = \frac{3}{2}$$.
- Площадь поверхности шара: $$S = 4\pi R^2 = 9\pi$$.
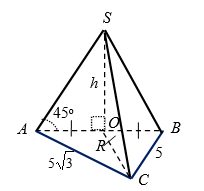
Если основанием треугольной пирамиды является прямоугольный треугольник с катетами $$5$$ и $$5\sqrt{3}$$, а боковые ребра пирамиды наклонены к плоскости основания под углом $$45^{\circ}$$, то высота пирамиды равна:
На рисунке 2 точка $$O$$ – центр окружности, описанной около основания пирамиды.
По теореме Пифагора: $$AB = \sqrt{75 + 25} = 10$$.
Так как $$\angle SAO = 45^{\circ}$$, то $$\angle ASO = 90^{\circ} - 45^{\circ} = 45^{\circ}$$.
Следовательно, $$SO = AO = 5 = h$$.
Точки $$A$$, $$B$$ и $$C$$ удалены от некоторой плоскости соответственно на 45 см, 25 см и 20 см. Расстояние от точки пересечения медиан треугольника $$ABC$$ до данной плоскости (в дециметрах) равно:
- $$FP = \frac{BD}{2} = 2,5$$ (см) как средняя линия треугольника $$CBD$$.
- $$AK = AA_1 -MA_1 - KM = 45 - 20 -2,5 = 22,5$$ (см).
- Так как $$\frac{AK}{x} = \frac{3k}{x}$$, то $$\frac{22,5}{x} = \frac{3}{1}$$, откуда $$x = 7,5$$ (см).
- $$OO_1 = 7,5 + 2,5 + 20 = 30$$ (см).
На рисунке 9: $$AA_1 = 45$$ (см),
точка $$O$$ – точка пересечения медиан треугольника $$ABC$$.

Если диагональ прямоугольного параллелепипеда равна $$6$$ см, а смежные стороны его основания равны $$4$$ см и $$3$$ см, то объем параллелепипеда равен:
- По формуле $$d^2 = a^2 + b^2 + c^2$$ получим:
$$36 = 16 + 9 + c^2$$, откуда $$c = \sqrt{11}$$ см (рис. 1).
- По формуле $$V = a \cdot b \cdot c$$ получим:
$$V = 4 \cdot 3 \cdot \sqrt{11} = 12\sqrt{11}$$ ($$см^3$$).

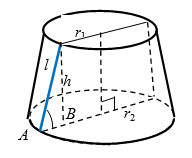
Образующая усеченного конуса длины $$10$$ наклонена к плоскости его основания под углом $$60^{\circ}$$. Если радиусы его оснований относятся как $$1 : 6$$, то площадь боковой поверхности конуса равна:
- Так как $$\angle A = 60^{\circ}$$ (рис. 3), то:
$$sin 60^{\circ} = \frac{h}{l}$$, откуда $$h = 5\sqrt{3}$$;
$$cos 60^{\circ} = \frac{AB}{l}$$, $$\frac{1}{2} = \frac{AB}{10}$$, откуда $$AB = 5$$.
- Так как $$r_2 = r_1 + 5$$ и $$\frac{r_1}{r_2} = \frac{1}{6}$$, то $$6r_1 = r_1 + 5$$,
откуда $$r_1 = 1$$, а $$r_2 = 6$$.
- Площадь боковой поверхности конуса:
$$S = \pi (r_1 + r_{2})l$$, $$S = \pi (1 + 6) \cdot 10 = 70\pi$$.
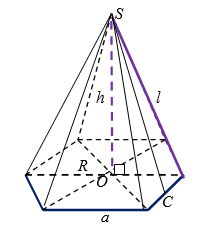
Правильная шестиугольная пирамида со стороной основания $$\frac{2\sqrt{3}}{3}$$ вписана в конус. Если образующая конуса в два раза больше его высоты, то боковая поверхность пирамиды равна:
- Найдем высоту конуса и пирамиды (рис. 5).
Так как $$R = a = \frac{2\sqrt{3}}{3}$$, а $$l = 2h$$, то $$4h^2 = h^2 + \frac{4}{3}$$,
откуда $$h = \frac{2}{3}$$, а $$l = \frac{4}{3}$$.
- Найдем апофему пирамиды:
$$SC = \sqrt{l^2 - \frac{a^2}{4}} = \sqrt{\frac{16}{9} - \frac{1}{3}} = \frac{\sqrt{13}}{3}$$.
- Найдем боковую поверхность пирамиды:
$$S = 2a \cdot SC = \frac{4\sqrt{3}}{3} \cdot \frac{\sqrt{13}}{3} = \frac{4\sqrt{39}}{9}$$.
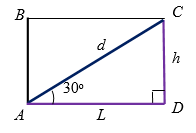
Если диагональ развертки боковой поверхности цилиндра равна $$4\sqrt[3]{\pi}$$ и образует угол $$30^{\circ}$$ с его основанием, то объем цилиндра равен:
- Так как $$\angle CAD = 30^{\circ}$$ (рис. 6), то $$h = \frac{d}{2} = 2\sqrt[3]{\pi}$$.
Тогда, $$AD = \sqrt{d^2 - h^2} = \sqrt{16\sqrt[3]{\pi^2} - 4\sqrt[3]{\pi^2}} = 2\sqrt[6]{27\pi^2}$$.
- Так как $$AD = L = 2\pi r$$, то $$2\pi r = 2\sqrt[6]{27\pi^2}$$, откуда $$r = \frac{\sqrt[6]{27\pi^2}}{\pi}$$.
- Объем цилиндра:
$$V = \pi r^2 h$$, $$V = \frac{\pi \sqrt[3]{27\pi^2} \cdot 2\sqrt[3]{\pi}}{\pi^2} = 6$$.
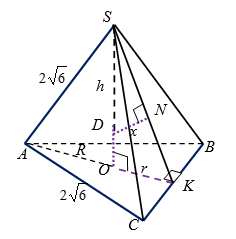
Если шар касается всех граней правильного тетраэдра, сторона основания которого равна $$2\sqrt{6}$$, то радиус шара равен:
- Радиус окружности, описанной около основания тетраэдра:
$$R = \frac{a}{\sqrt{3}} = \frac{2\sqrt{6}}{\sqrt{3}} = 2\sqrt{2}$$.
- Высота тетраэдра:
$$SO = \sqrt{a^2 - R^2} = \sqrt{24 - 8} = 4 = h$$.
- Радиус окружности, вписанной в основание тетраэдра:
$$r = \frac{a}{2\sqrt{3}} = \frac{2\sqrt{6}}{2\sqrt{3}} = \sqrt{2}$$.
- Апофема тетраэдра:
$$SK = \sqrt{h^2 + r^2} = \sqrt{16 + 2} = 3\sqrt{2}$$.
- Так как $$\bigtriangleup SND \sim \bigtriangleup SOK$$, то
$$\frac{ND}{OK} = \frac{SD}{SK}$$, $$\frac{x}{\sqrt{2}} = \frac{4 - x}{3\sqrt{2}}$$, откуда $$x = 1$$.
На рисунке 8: точка $$D$$ – центр шара, $$x$$ – радиус шара.
Полукруг вращается вокруг своего диаметра длины $$5$$. Объем тела вращения равен:
Тело вращения: шар.
Так как $$R = \frac{5}{2}$$, то $$V = \frac{4\pi R^3}{3} = \frac{4\pi \cdot 125}{3 \cdot 8} = \frac{125\pi}{6}$$.

