Многогранники ИТ
Основание пирамиды – ромб с острым углом $$30^{\circ}$$ и площадью $$50$$. Если двугранные углы при основании пирамиды равны, а ее высота равна $$5\sqrt{3}$$, то площадь боковой поверхности пирамиды равна:
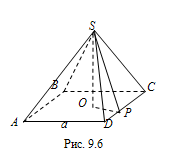
На рисунке 9.6:
точка $$O$$ – центр вписанной окружности;
$$SO=h=5\sqrt{3}$$ ;
$$SP$$ – высота боковой грани, так как $$OP\perp DC$$.
- Найдем сторону ромба: $$50=a^{2}sin30^{\circ}$$ , $$50=a^{2}\cdot \frac{1}{2}$$ , $$a=10$$.
- Найдем высоту ромба: $$S=ah$$ , $$50=10h$$, $$h=5$$. Тогда радиус окружности, вписанной в ромб, равен $$2,5$$ – на рисунке 9.6 отрезок $$PO$$.
- Найдем высоту боковых граней пирамиды: $$SP=\sqrt{OP^{2}+SO^{2}}$$, $$SP=\sqrt{\frac{25}{4}+75}$$, $$SP=5\sqrt{\frac{1}{4}+3}=\frac{5\sqrt{13}}{2}$$.
- Найдем боковую поверхность пирамиды: $$S_{bok.}=\frac{1}{2}\cdot 4a\cdot SP$$, $$S_{bok.}\frac{1}{3}\cdot 40\cdot \frac{5\sqrt{13}}{2}=50\sqrt{13}$$.
- Двугранным углом при основании пирамиды называют угол между плоскостью ее боковой грани и плоскостью основания пирамиды.
- В нашем случае пирамида не является правильной, но боковые грани – равные треугольники, поэтому справедливо, что $$S$$бок.$$=\frac{1}{2}P$$осн.$$\cdot h$$бок.
Основание пирамиды – равнобокая трапеция с углом $$30^{\circ}$$, а все боковые грани образуют с плоскостью основания углы, тангенс которых равен $$ 1,5\sqrt{3}$$.
Если высота пирамиды равна $$3\sqrt{3}$$ , то площадь ее основания равна:
$$ABCD$$;
$$PO=r$$ – радиус окружности, вписанной в трапецию; $$SP\perp AD$$ по теореме о трех перпендикулярах.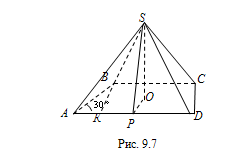
В четырехугольник можно вписать окружность, если суммы длин его противолежащих сторон равны.
Если радиус окружности, описанной около грани правильного тетраэдра, равен $$\frac{2}{\sqrt{3}}$$, то объем тетраэдра равен:
- Треугольную пирамиду называют тетраэдром. Тетраэдр называется правильным, если все его ребра равны.
- Радиус окружности, описанной около правильного треугольника со стороной $$a$$: $$R=\frac{a}{\sqrt{3}}$$ .
- Площадь правильного треугольника со стороной $$a$$: $$S=\frac{\sqrt{3}a^{2}}{4}$$ .
- Объем пирамиды: $$V=\frac{1}{3}S$$осн.$$h$$ .
-
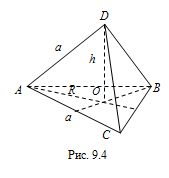
Зная, что $$R=\frac{2}{\sqrt{3}}$$, найдем ребро тетраэдра:
$$\frac{2}{\sqrt{3}}=\frac{a}{\sqrt{3}}$$ , $$a=2$$ (рис. 9.4).
- Найдем высоту пирамиды: $$DO=\sqrt{DA^{2}-OA^{2}}$$, $$DO=\sqrt{4-\frac{4}{3}}=\sqrt{\frac{8}{3}}=\frac{2\sqrt{2}}{\sqrt{3}}$$.
- Найдем площадь основания пирамиды: $$S=\frac{\sqrt{3}\cdot 4}{4}=\sqrt{3}$$.
- Найдем объем пирамиды: $$V=\frac{1}{3}\cdot \sqrt{3}\cdot \frac{2\sqrt{2}}{\sqrt{3}}=\frac{2\sqrt{2}}{3}$$.
Различайте правильную треугольную пирамиду и правильный тетраэдр.
У правильной треугольной пирамиды основание – правильный треугольник, а боковые ребра хоть и равны между собой, но не обязательно, что они равны ребрам основания пирамиды.
Правильный тетраэдр – это треугольная пирамида, у которой все ребра равны.
Боковое ребро правильной четырехугольной усеченной пирамиды наклонено к плоскости основания под углом $$45^{\circ}$$ . Если площади оснований пирамиды равны $$8$$ и $$32$$, то ее утроенный объем равен:
- Усеченной пирамидой называют многогранник, вершинами которого служат вершины основания пирамиды и вершины ее сечения плоскостью, параллельной основанию пирамиды. Основания усеченной пирамиды – подобные многоугольники.
- Площадь квадрата с диагональю $$d$$: $$S=\frac{d^{2}}{2}$$.
- Объем усеченной пирамиды находят по формуле: $$V=\frac{1}{3}h(S_{1}+S_{2}+\sqrt{S_{1}S_{2}})$$, где $$S_{1}$$ и $$S_{2}$$ – площади оснований, $$h$$ – ее высота.
-
Диагональное сечение пирамиды – равнобокая трапеция $$ABCD$$ (рис. 9.8).
- Так как основания усеченной пирамиды – квадраты и площади их соответственно равны $$8$$ и $$32$$, то: 1) $$8=\frac{d_{1}^{2}}{2}$$, откуда $$d_{1}=4$$ , а $$\frac{d_{1}}{2}=2$$; 2) $$32=\frac{d_{2}^{2}}{2}$$, откуда $$d_{2}=8$$, а $$\frac{d_{2}}{2}=4$$.
- Тогда: $$DP=OD-OP$$, $$DP=\frac{d_{2}}{2}-\frac{d_{1}}{2}$$, $$DP=4-2=2$$.
- Треугольник $$CPD$$ – равнобедренный ($$\angle C=\angle D=45^{\circ}$$). Значит, $$CP=2=h$$.
- Найдем объем пирамиды: $$V=\frac{1}{3}\cdot 2(8+32+\sqrt{8\cdot 32})$$, $$V=\frac{2}{3}\cdot (40+16)=\frac{112}{3}$$.
- Тогда, $$3V=112$$.
Если пирамида правильная, то ее основание – правильный многоугольник.
Если большая диагональ правильной шестиугольной призмы равна $$2$$ и образует с высотой угол $$60^{\circ}$$, то площадь боковой поверхности призмы равна:
Площадь боковой поверхности прямой призмы высоты $$h$$ находят по формуле:
$$S$$бок.$$=P$$осн.$$\cdot h$$.Тогда $$\angle CAD=30^{\circ}$$, а $$CD=1$$ (как катет, лежащий против угла $$30^{\circ}$$).
Тогда, $$S_{bok.}=6a\cdot h$$, $$S_{bok.}=6\cdot \frac{\sqrt{3}}{2}\cdot 1=3\sqrt{3}$$.
- Правильной призмой называют прямую призму, основанием которой является правильный многоугольник.
- Диагональю призмы называют отрезок, соединяющий две ее вершины, не принадлежащие одной грани.
Если основанием треугольной пирамиды является прямоугольный треугольник с катетами $$6$$ и $$8$$, а все боковые ребра пирамиды наклонены к плоскости основания под углом $$45^{\circ}$$, то объем пирамиды равен:
- Если все боковые ребра пирамиды равны (или наклонены к плоскости основания пирамиды под одним и тем же углом), то высота пирамиды опускается в центр окружности, описанной около ее основания.
- Площадь прямоугольного треугольника с катетами $$a$$ и $$b$$: $$S=\frac{ab}{2}$$ .
- Объем пирамиды: $$V=\frac{1}{3}S$$осн.$$\cdot h$$ .
Высота пирамиды опускается в центр окружности, описанной около прямоугольного треугольника $$ABC$$, точку $$O$$, расположенную на середине гипотенузы $$AB$$ (рис. 9.5).

Центр окружности, описанной около прямоугольного треугольника, расположен на середине его гипотенузы.
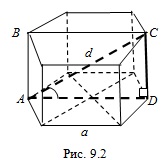
Если диагональ прямоугольного параллелепипеда равна $$\sqrt{58}$$, а его измерения относятся как $$2:3:4$$, то объем параллелепипеда равен:
- Прямоугольным параллелепипедом называют прямой параллелепипед, основанием которого является прямоугольник.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений: $$d^{2}=a^{2}+b^{2}+c^{2}$$, где $$a,b,c$$ – длины ребер, выходящих из одной вершины, $$d$$ – диагональ параллелепипеда.
- Объем прямоугольного параллелепипеда с измерениями $$a,b$$ и $$c$$ находят по формуле: $$V=abc$$ .
Пусть коэффициент пропорциональности равен $$k$$.
Запишем измерения параллелепипеда:
$$a=2k$$, $$b=3k$$ и $$c=4k$$.По свойству диагонали параллелепипеда:
$$58=4k^{2}+9k^{2}+16k^{2}$$, $$29k^{2}=58$$, $$k^{2}=2$$, $$k=\sqrt{2}$$.Тогда, $$V=abc=24k^{3}=48\sqrt{2}$$.
Длины ребер, выходящих из одной вершины параллелепипеда, называют его измерениями.
Если радиус окружности, описанной около грани куба, равен $$\sqrt{6}$$ , то площадь поверхности куба равна:
- Радиус окружности, описанной около квадрата со стороной $$a$$: $$R=\frac{d}{2}$$ .
- Площадь квадрата со стороной $$a$$ и диагональю $$d$$: $$S=a^{2}$$; $$S=\frac{1}{2}d^{2}$$.
- Площадь поверхности куба с ребром $$a$$: $$S$$пов.$$= 6a^{2}$$.
- Так как грань куба – квадрат и $$R=\sqrt{6}$$ , то $$\sqrt{6}=\frac{d}{2}$$ , а $$d=2\sqrt{6}$$ – диагональ квадрата.
- Найдем площадь квадрата: $$S=\frac{1}{2}d^{2}$$, $$S=\frac{1}{2}(2\sqrt{6})^{2}=12=a^{2}$$.
- Тогда, $$S$$пов.$$=6\cdot 12=72$$.
Все ребра куба равны, а поверхность куба состоит из шести равных квадратов.
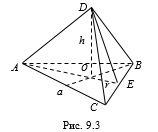
Если высота правильной треугольной пирамиды равна $$4$$, а сторона ее основания равна $$6\sqrt{3}$$, то длина апофемы равна:
На рисунке 9.3 $$OE=r=3$$.
Теорема о трех перпендикулярах: для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы она была перпендикулярна проекции этой наклонной на плоскость.
Если стороны основания параллелепипеда имеют длины $$3$$ и $$\sqrt{3}$$ образуют угол $$60^{\circ}$$, а его боковое ребро длины $$6$$ наклонено к плоскости основания под углом $$30^{\circ}$$, то объем параллелепипеда равен:
- Параллелепипедом называют призму, все грани которой параллелограммы.
- Объем наклонной призмы высоты $$h$$ можно вычислить по формуле: $$V=S$$осн.$$\cdot h$$.
- Площадь параллелограмма можно вычислить по формуле: $$S=ab \cdot sin\alpha$$, где $$a,b$$ – смежные стороны, $$\alpha$$ – острый угол.
На рисунке 9. 1:
$$AA_{1}=6$$ , $$\angle A_{1}AO=30^{\circ}$$ .
Тогда, $$A_{1}O=3$$ (как катет, лежащий против угла $$30^{\circ}$$ ).
Площадь основания:
$$S=3\sqrt{3}sin60^{\circ}$$, $$S=3\sqrt{3}\cdot \frac{\sqrt{3}}{2}=\frac{9}{2}$$.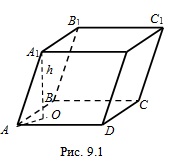
Высотой призмы называется отрезок перпендикуляра, заключенный между основаниями призмы. Если призма прямая, то ее боковые ребра – высоты.