Случайные величины ИТ /testy

Случайные величины ИТ

Распределение дискретной случайной величины $$X$$ задано таблицей:

Математическое ожидание $$CBX$$ равно:

Математическое ожидание дискретной $$CBX$$ находят по формуле:
$$M(X)=x_1p_1+x_2p_2+x_3p_3+...+x_np_n$$.

$$M(X)=-0,1\cdot 0,2+0,1\cdot 0,1+0,2\cdot 0,3+0,3\cdot 0,1+0,5\cdot 0,3$$,
$$M(X)=-0,02+0,01+0,06+0,03+0,15=0,23$$.

Математическое ожидание $$CBX$$ – это среднее значение величины $$X$$ или центр ее распределения.

Введите ответ в поле

Известна функция распределения случайной величины $$F(x)=\begin{cases} 0,x\leq 0 ,\\ \textrm{sin} {x},0 < x\leq 0,5\pi,\\1, x > 0,5\pi.\end{cases}$$
Вероятность того, что $$CBX$$ примет значение из промежутка $$[0,5\pi;\pi)$$ , равна:

Вероятность того, что непрерывная $$CBX$$ примет значение из промежутка $$[\alpha; \beta )$$ можно найти по формуле: $$P(\alpha \leq X < \beta)=F(\beta)-F(\alpha)$$.

Так как при $$x=0,5\pi$$ функция распределения имеет вид $$F(x)=sinx$$ ,

а при $$x=\pi$$ функция распределения имеет вид $$F(x)=1$$ , то:

$$p=P(0,5\pi \leq X<\pi)$$,

$$p=F(\pi)-F(0,5\pi)$$,

$$p=1-sin0,5\pi$$ ,

$$p=1-1=0$$.

Вероятность того, что непрерывная $$CBX$$примет значения из промежутков $$(\alpha; \beta )$$ , $$[\alpha; \beta ]$$ и $$(\alpha; \beta ]$$ также находят по формуле:

$$P(\alpha \leq X < \beta)=F(\beta)-F(\alpha)$$ ,

так как вероятность того, что $$CBX$$ примет только одно значение из заданного промежутка, равна нулю: $$P(X=\alpha)=0$$ , $$P(X=\beta)=0$$ .

Введите ответ в поле

Распределение системы случайных величин $$X$$ и $$Y$$ представлено в таблице:

Ковариация случайных величин равна:

Математические ожидания дискретных случайных величин, входящих в систему, находят по формулам:

$$M(X)=\sum ^m_{i=1}\sum ^n_{j=1}x_ip_{ij}$$ , $$M(Y)=\sum ^m_{i=1}\sum ^n_{j=1}y_jp_{ij}$$ .

Ковариацию $$CBX$$ и $$CBY$$ можно найти по формуле:

$$cov(X,Y)=M(XY)-M(X)M(Y)$$.

Найдем математическое ожидание $$CBX$$:
$$M(X)=0\cdot 0,6+1\cdot 0,4=0,4$$.
2. Найдем математическое ожидание $$CBY$$:
$$M(Y)=1\cdot 0,3+2\cdot 0,2+3\cdot 0,5=2,2$$.
3. Найдем $$M(XY)$$, перемножая соответствующие значения $$X$$, $$Y$$, $$p$$ и складывая полученные произведения:
$$M(XY)=0\cdot 1\cdot 0,1+0\cdot 2\cdot 0,1+0\cdot 3\cdot 0,4+1\cdot 1\cdot 0,2+1\cdot 2\cdot 0,1+1\cdot 3\cdot 0,1=0,7$$.
4. Найдем ковариацию:
$$cov(X,Y)=0,7-0,4\cdat 2,2= -0,18$$.

Ковариацией двух случайных величин $$X$$ и $$Y$$ называют математическое ожидание произведения их отклонений от своих математических ожиданий:

$$cov(X;Y)=M((X-M(X))(Y-M(Y)))$$.

Введите ответ в поле

Если случайная величина задана функцией распределения
$$F(x)=\begin{cases} 0,x\leq -0,5\pi,\\cosx,-0,5\pi < x\leq 0,\\1, x > 0,\end{cases}$$

то функция плотности распределения вероятностей имеет вид:

$$p(x)=F'(x)$$.

$$p(x)=\begin{cases} 0',x\leq -0,5\pi ,\\ (cosx)',-0,5\pi< x\leq 0,\\1',x>0. \end{cases}$$

$$p(x)=\begin{cases} 0,x\leq -0,5\pi ,\\ -sinx,-0,5\pi < x\leq 0,\\ 0,x > 0. \end{cases}$$

Плотностью распределения непрерывной случайной величины $$X$$ в точке $$x$$ называют функцию: $$p(x)=\lim_{\Delta x\rightarrow 0}\frac{P(x\leq X < x+ \Delta x)}{\Delta x}$$

Выберите один из вариантов

$$p(x)=\begin{cases} 0,x\leq -0,5\pi ,\\ -\textrm{sin} {x},-0,5\pi < x\leq 0,\\ 0,x > 0. \end{cases}$$

$$p(x)=\begin{cases} 0,x\leq -0,5\pi ,\\ \textrm{sin} {x},-0,5\pi < x\leq 0,\\ 0,x > 0. \end{cases}$$

$$p(x)= \textrm{sin} {x}$$

$$p(x)=-\textrm{sin} {x}$$

$$p(x)=0$$

Распределение дискретной случайной величины $$X$$ задано таблицей:

Значение $$k$$ равно:

Говорят, что задан закон распределения случайной величины $$X$$, если каждому значению $$x$$ поставлена в соответствие вероятность появления и сумма всех вероятностей равна числу $$1$$.

Так как сумма всех вероятностей равна числу $$1$$, то
$$0,11+0,19+0,2+0,1+3k+k=1$$
откуда $$0,6+4k=1$$, $$4k=0,4$$ $$k=0,1$$.

Виды случайных величин:
1) дискретная $$CBX$$;– принимает конечное или счетное множество значений;
2) непрерывная $$CBX$$– принимает все значения из заданного промежутка.

Введите ответ в поле

Случайная величина $$X$$ задана функцией плотности распределения вероятностей $$p(x)=\begin{cases} 0,x\leq 0 ,\\ x, 0 < x\leq 1,\\0, x > 1.\end{cases}$$
Среднее квадратическое отклонение $$CBX$$ равно:

Дисперсию непрерывной $$CBX$$ с плотностью распределения $$p(x)$$, все значения которой принадлежат отрезку $$[\alpha; \beta]$$ находят по формуле:
$$D(X)=\int_{\alpha }^{\beta }x^2p(x)dx-(M(X))^2$$.

Найдем математическое ожидание $$CBX$$:
$$M(X)=\int_{0}^{1}x^2dx=\frac{x^3}{3}|_{0}^{1}=\frac{1}{3}$$.
Найдем дисперсию $$CBX$$:
$$D(x)=\int_{0}^{1}x^3dx-\left ( \frac{1}{3} \right )^2$$,
$$D(x)=\frac{x^4}{4}|_{0}^{1}-\frac{1}{9}=\frac{5}{36}$$.
Найдем среднее квадратическое отклонение $$CBX$$:
$$\sigma (X)=\sqrt{\frac{5}{36}}=\frac{\sqrt{5}}{6}$$.

Еcли все значения $$CBX$$ принадлежат промежутку $$(-\infty ;+\infty )$$ , то $$D(X)=\int_{-\infty }^{+\infty }x^2p(x)dx-(M(X))^2$$ , при условии, что интеграл сходится.

Выберите один из вариантов

$$0,5$$

$$\frac{\sqrt{5}}{6}$$

$$\frac{5}{26}$$

$$1$$

$$0,36$$

Случайная величина $$X$$ задана функцией распределения $$F(x)=\begin{cases}0,x\leq -0,5, \\ 2x+1, -0,50 < x\leq 0,\\1, x > 0.\end{cases}$$
Математическое ожидание равно:

Математическое ожидание непрерывной $$CBX$$ с плотностью распределения $$p(x)$$, все значения которой принадлежат отрезку $$[\alpha ;\beta ]$$ , находят по формуле:
$$M(X)=\int_{\alpha }^{\beta }xp(x)dx$$.

Если все значения $$CBX$$ принадлежат промежутку $$(-\infty ;+\infty )$$ , то $$M(X)=\int_{-\infty }^{+\infty }xp(x)dx$$ , при условии, что интеграл сходится.

Введите ответ в поле

Известна функция плотности вероятностей $$p(x)=\begin{cases} 0,x\leq 0 ,\\ \textrm{cos} {x},0 < x\leq 0,5\pi,\\ 0,x > 0,5\pi. \end{cases}$$
Вероятность того, что $$CBX$$ примет значение из промежутка $$[0,25\pi;0,5\pi]$$ , равна:

Вероятность того, что непрерывная $$CBX$$ примет значение из промежутка $$[\alpha;\beta)$$ можно найти по формуле:$$P(\alpha \leq X<\beta )=\int_{\alpha }^{\beta }p(x)dx$$.

Так как при $$0,25\pi \leq x\leq 0,5\pi$$ функция плотности вероятностей имеет вид $$p(x)=cosx$$ , то:

$$p=\int_{0,25\pi}^{0,5\pi}cosxdx$$,

$$p=sinx|_{0,25\pi}^{0,5\pi}$$,

$$p=sin0,5\pi-sin0,25\pi$$,

$$p=1-\frac{\sqrt{2}}{2}$$.

Вероятность того, что непрерывная $$CBX$$ примет значения из промежутков $$(\alpha ;\beta )$$ , $$(\alpha ;\beta ]$$ и $$[\alpha ;\beta ]$$ также находят по формуле:

$$P(\alpha \leq X<\beta )=\int_{\alpha }^{\beta }p(x)dx$$ .

Выберите один из вариантов

$$0$$

$$1$$

$$0,7$$

$$1-0,5\sqrt{2}$$

$$0,5\sqrt{2}$$

Распределение дискретной случайной величины $$X$$ задано таблицей:

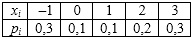
Дисперсия $$CBX$$ равна:

Дисперсию дискретной $$CBX$$ можно найти по формуле:
$$D(X)=M(X^2)-M^2(X)$$
где $$M(X)=x_1p_1+x_2p_2+x_3p_3+...+x_np_n$$
$$M(X^2)=x_1^2p_1+x_2^2p_2+x_3^2p_3+...+x_n^2p_n$$.

Найдем математическое ожидание $$CBX$$:
$$M(X)=-1\cdot 0,3+0\cdot 0,1+1\cdot 0,1+2\cdot 0,2+3\cdot 0,3$$,
$$M=-0,3+0+0,1+0,4+0,9=1,1$$
Найдем математическое ожидание квадрата $$CBX$$:
$$M(X^2)=(-1)^2\cdot 0,3+0^2\cdot 0,1+1^2\cdot 0,1+2^2\cdot 0,2+3^2\cdot 0,3$$,
$$M (X^2)=0,3+0+0,1+0,8+2,7=3,9$$
Найдем дисперсию $$CBX$$: $$D(X)=3,9-1,1^2=2,69$$.

Дисперсия или рассеивание $$CBX$$ – это математическое ожидание квадрата отклонения величины $$X$$ от ее математического ожидания:
$$D(X)=M(X-M(X))^2$$.

Введите ответ в поле

Распределение случайной величины $$X$$ задано таблицей:

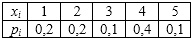
Вероятность того, что $$CBX$$ примет значение, не меньшее чем $$3,5$$, равна:

Вероятность того, что дискретная $$CBX$$ примет значение из заданного промежутка равна сумме вероятностей всех ее значений, принадлежащих данному промежутку.

Так как промежутку $$[3,5;+\infty )$$ принадлежат два значения $$CBX$$ $$4$$ и $$5$$, то:
$$p=P(3,5\leq X< +\infty)$$,
$$p=P(X=4)+P(X=5)$$,
$$p=0,4+0,1=0,5$$.

Распределение дискретной $$CBX$$ всегда можно представить в таблице.

Введите ответ в поле